Течение идеальной жидкости. Уравнение непрерывности

 

В отличие от твердых тел, жидкости и газы, с точки зрения механики, являются веществами текучими. Но если в твердых телах пластичность неотделима от диссипации, то в случае текучей среды диссипацией при рассмотрении многих важных процессов и явлений можно пренебречь. Такой подход называется приближением идеальной жидкости (заметим, что во многих случаях приближение идеальной жидкости описывает и динамику течения газа). Далее, очень многие практически важные задачи допускают представление несжимаемой жидкости. Это понятие вошло в обиход и нередко используется в технических приложениях, но надо отдавать себе отчет в том, что сжимаемость жидкости, если понимать ее в контексте гл. 8.1, заметно превышает таковую у твердого тела. Но как твердое тело — вполне реальное и подверженное деформациям — можно во многих динамических задачах с хорошей точностью считать абсолютно твердым, так и жидкость в задаче о ее течении нередко с достаточной точностью представима как несжимаемая. Обычно такое представление оправдано, если перепады

скоростей в жидкости гораздо меньше скорости звука, и в этом смысле даже воздух при атмосферном давлении может рассматриваться как несжимаемая жидкость, если скорость его течения меньше 300 м/с.

Хотя, казалось бы, течение жидкости и движение тела конечных размеров весьма различаются, общий характер в системе основных понятий все же существует. Если мы выделим объем жидкости столь малый, что можно пренебречь его размерами и формой, и этот объем не перемешивается на характерном масштабе задачи (или за характерное время задачи) с другим веществом, то такой жидкий элемент можно рассматривать как материальную точку. Это позволяет определить скорость и ускорение элемента и вывести

на этой основе уравнения течения (или, в частности, равновесия) жидкости.

Траектория такого жидкого элемента называется линией тока (рис. 8.6 а).

Совокупность линий тока, близлежащих в пределах, заданных характерным

 

 

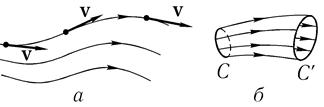
Рис. 8.6 Траектория жидкого элемента называется линией тока

Совокупность линий тока, близлежащих в пределах, заданных характерным временем и масштабом задачи, называется трубкой тока

Трубка тока охватывается некоторым односвязным контуром

 

временем и масштабом задачи, называется трубкой тока. Предполагается, что трубка тока охватывается некоторым односвязным контуром (С —>• С' на рис. 8.6 б). Корректность понятий жидкого элемента и линии тока обусловлена лишь малостью элементарного объема. Понятие трубки тока подразумевает, что на интересующем нас пространственном масштабе линии тока достаточно мало расходятся и, в частности, не образуют вихрей.

При таком рассмотрении локальные характеристики — плотность вещества ρ и скорость

v — принято относить не к движущемуся жидкому элементу, а к потоку в целом и рассматривать как функции точки ρ(r), v(r).

Если протекание вещества не сопровождается никакими реакциями, то масса вещества в потоке сохраняется. Рассмотрим некоторую трубку тока (рис. 8.7 а). Пусть течение стационарно.

Выделим объем, ограниченный стенками трубки тока и двумя ее сечениями, нормальными к скорости жидкости. Сокражение массы в выделенном объемме выражается равенством массы жидкости, втекающей в сечение 1 и вытекающей из сечения 2 за время dt:

 

 

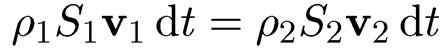
Здесь ρ_1,2, S_1,2 , v_1,2 - плотность жидкости,

 

 

Рис. 8.7

площадь нормального сечения трубки тока и скорость жидкости в точках 1 и 2. Тем самым закон сохранения массы принимает вид уравнения неразрывности струи

ρS_┴v = const (8.13)

или для несжимаемой жидкости (ρ = const)

S_┴v = const. (8.14)

Если поток нестационарен, уравнения (8.13, 8.14) должны быть модифицированы. Представим себе одномерную трубку тока (рис. 8.7 б). Закон сохранения массы вещества означает, что масса жидкости, втекающая в некоторый объем, ρv(x) dtS, равна массе жидкости, накапливающейся в этом объеме, ρdtS dx, плюс массе вытекающей жидкости ρv(x + dx) dtS. Имея в виду, что все характерные параметры зависят, вообще говоря, от двух переменных х и t, введем понятие частной производной

 

∂f(x, t)/∂t = (∂f/∂t)|_x=const, ∂f(x,t)/∂x = (∂f/∂x)|_{t = const}.

 

Закон сохранения массы принимает вид

ρv(x)dtS = ρ^!Sdx + ρv(x + dx) dtS =>

∂ρ/∂t = -∂(ρv(x))/∂x.

 

Традиционная форма записи этого закона называется уравнением непрерывности:

 

∂ρ/∂t + ∂(ρv)/∂x = 0. (8.15)

 

В случае неодномерного течения обобщение уравнения (8.15) достигается

посредством введения оператора дивергенции. По определению, для любой

векторной функции j(r) = j(x, у, z) дивергенция j есть

 

div j = ∂j_x/∂x + ∂j_y/∂у + ∂j_z/∂z.

 

В общем случае трехмерного течения уравнение (8.15) принимает вид

 

∂ρ/∂t + div (ρv) =0. (8.16)

 

Если же справедливо приближение несжимаемой жидкости, то изменением

плотности как в пространстве, так и во времени можно пренебречь:

 

div v = 0. (8.17)

 

Уравнения (8.16), (8.17) выглядят, конечно, сложнее, чем, соответственно,

(8.13), (8.14), но обладают и заметным преимуществом — они локальны,

т. е. не привязаны ни к какой трубке тока, и их решение, в принципе, просто

некоторая функция точки в пространстве r и времени t.