Силы упругости и трения, в отличие от гравитационных сил, появляются только при соприкосновении тел.
Силы упругости являются следствием деформации, возникающей при контакте тел (см. §8). На карандаш, лежащий на столе, действует сила тяжести, однако, он остаётся неподвижным, и значит, на него действует сила упругости чуть-чуть деформированного им стола, направленная вертикально вверх и равная по величине силе тяжести карандаша. Если на то же место стола поставить монитор компьютера, то деформацию поверхности стола можно будет заметить и на глаз.
Деформации возникают только тогда, когда одни участки тела перемещаются относительно других. Так, часть колеса автомобиля, соприкасающаяся с землёй, деформируется, смещаясь относительно других (см. рис.10г). При движении автомобиля наступает момент, когда данная часть колеса перестаёт соприкасаться с землёй и её деформация исчезает. Такие тела, деформации которых исчезают после прекращения действия сил, называют упругими. Однако во многих случаях тело не восстанавливает своей первоначальной формы после окончания взаимодействия с другим телом. Такие тела называют пластичными. Следы, оставляемые нами на мокром песке, могут служить примером пластичной деформации.
Силы упругости растут при увеличении деформации. Особенно наглядно это можно продемонстрировать, растягивая пружину (см. рис.13а). Видно, что удлинение пружины прямо пропорционально массе подвешенного груза. Таким образом, модуль силы упругости F, прямо пропорционален изменению длины пружины DL. Это заключение, впервые сформулированное Р. Гуком, справедливо не только для пружин, но и для любых малых упругих деформаций (сжатий или растяжений) тел. Закон Гука в математической форме записывается следующим образом:
F = k. DL (13.1)
где k – коэффициент упругости или жёсткости. Чем больше k, тем труднее деформировать данное тело.
Силы трения, как и упругие силы, возникают при контакте двух тел, а именно при движении одного тела по поверхности другого. При скольжении неровности (микробугорки) поверхности одного тела цепляются за неровности другого, что приводит к возникновению упругих сил, тормозящих движение. Если же эти неровности практически отсутствуют, как происходит, например, при скольжении листа стекла по стеклу, то тела начинают прилипать друг к другу из-за образования связей между молекулами соприкасающихся поверхностей тел.
Чтобы сдвинуть тело, находящееся на поверхности другого тела (см. рис.13б), необходимо приложить силу F, достаточную для (1) преодоления упругих сил, возникших при деформации микробугорков поверхностей и (2) разрыва образовавшихся связей между молекулами контактирующих тел. Если сила F, оказывается меньше необходимой, то тело остаётся в покое, а значит, на это тело, кроме силы F, действует ещё одна сила, которую называют силой трения покоя FТП (см. рис. 13б), которая компенсирует действие силы F. Однако сила трения покоя не может превышать своего максимального значения Fmax , зависящего от свойств скользящих поверхностей, и силы, с которой их прижимают друг к другу. Поэтому, чтобы сдвинуть тело, необходимо приложить силу F>Fmax .
Результаты многих экспериментов показывают, что максимальное значение силы трения покоя, Fmax прямо пропорционально величине силы, прижимающей тела друг к другу (силе реакции опоры), N, что можно записать в виде:
Fmax = mТП.N, (13.2)
где mТП – коэффициент трения покоя.
Силу, препятствующую, скольжению одного тела по другому, называют силой трения скольжения. Сила трения скольжения, FТС всегда направлена в сторону, противоположную относительной скорости движения тел, и тоже прямо пропорциональна силе реакции опоры, N, или
FТС = mТС.N, (13.3)
где mТС – коэффициент трения скольжения. Установлено, что при малых скоростях относительного движения тел mТП и mТП мало отличаются друг от друга.
Вопросы для повторения:
· Чем отличаются силы упругости и трения от гравитационных сил?
· Чем отличаются упругие деформации от пластичных?
· Сформулируйте закон Гука.
· Как возникает сила трения, и от чего она зависит?
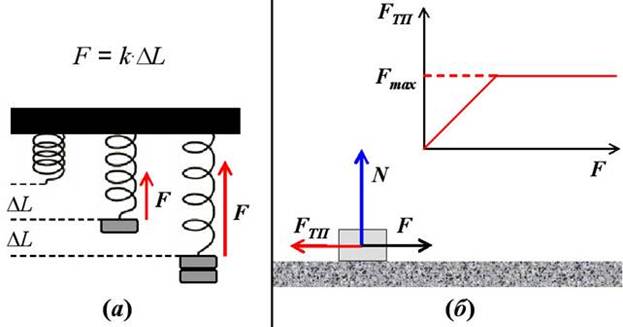
Рис.13. (а) – закон Гука, зависимость упругой силы F от деформации DL; (б) – зависимость силы трения покоя FТП от силы F, пытающейся сдвинуть тело с места вправо.
§ 14. ИМПУЛЬС ТЕЛА. ЗАМКНУТЫЕ СИСТЕМЫ. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
Используя законы Ньютона можно решить любые механические задачи. Однако применить эти законы бывает гораздо легче, если ввести понятие импульса тела, которым называют произведение массы тела на его скорость.
Пусть сила F начинает действовать на тело m, движущееся со скоростью v1. По второму закону Ньютона тело сразу начнёт двигаться с ускорением a=F/m , и через промежуток времени Dt его скорость станет равной v2=v1+a.Dt. При этом будет справедливо следующее равенство:
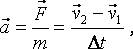
откуда следует, что

Таким образом, изменение вектора импульса тела, произошедшее за промежуток времени Dt, равно произведению вектора силы на время её действия. При этом вектор импульса изменяется только в том направлении, в котором действует сила.
До сих пор мы рассматривали движение какого-нибудь одного тела и действие сил на это тело. Часто, однако, приходится рассматривать движение сразу нескольких взаимодействующих тел, например, соударение бильярдных шаров, движение планет солнечной системы или стыковка двух космических аппаратов. В каждом из этих случаев мы изучаем не одно тело, а систему, состоящую из нескольких взаимодействующих между собой тел. При этом существуют такие системы, тела в которых взаимодействуют только между собой, и можно считать, что никакие внешние силы на такие системы не действуют. Такие системы тел называют замкнутыми или изолированными. Солнечную систему можно считать замкнутой системой тел, так как она очень удалена от других космических тел нашей Галактики.
Рассмотрим, как меняется импульс замкнутой системы, состоящей из двух тел – А и Б, при их столкновении. Согласно третьему закону Ньютона, сила F, с которой тело А действует на тело Б, равна по величине и противоположна по направлению силе, с которой тело Б действует на тело А. Поэтому для каждого из тел можно записать уравнение, аналогичное (14.1), где индексы А и Б указывают на то, что оно написано для тел А и Б, соответственно:
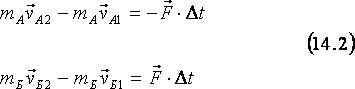
Складывая уравнения в (14.2), получаем:
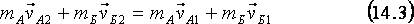
В правой части уравнения (14.3) стоит суммарный импульс системы до столкновения, а в левой – он же, но после. Таким образом, суммарный импульс тел замкнутой системы не изменяется в результате взаимодействия тел этой системы. Этот вывод, справедливый для любых замкнутых систем, называют законом сохранения импульса.
Применим закон сохранения импульса к решению задачи о неупругом столкновении двух шаров, сделанных, например, из пластилина, при условии, что после столкновения они движутся, как единое целое (см. рис. 14а). Считая систему из двух шаров замкнутой, приравниваем значения суммарных импульсов системы до и после столкновения (см. 14.3):
откуда можно легко найти скорость движения v слипшихся шаров после их неупругого столкновения.
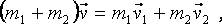
Закон сохранения импульса можно использовать для вычисления скорости v1 отдачи пушки массой m1 после выстрела снарядом массы m2 со скоростью v2 (см. рис. 14б). Система, состоящая из пушки и снаряда, не является замкнутой, т.к. на неё действует сила притяжения Земли. Однако в горизонтальном направлении на эту систему не действуют внешние силы, если пренебречь силами трения. Поэтому, применяя закон сохранения горизонтальной составляющей импульса системы и считая, что импульс системы до выстрела был равен нулю, имеем:
m1v1x + m2v2x = 0 ,
откуда можно вычислить скорость v1x отдачи пушки после выстрела.
Вопросы для повторения:
· Дайте определение импульса тела.
· Как изменяется импульс тела при действии силы?
· Какие системы тел называют замкнутыми?
· Сформулируйте закон сохранения импульса.
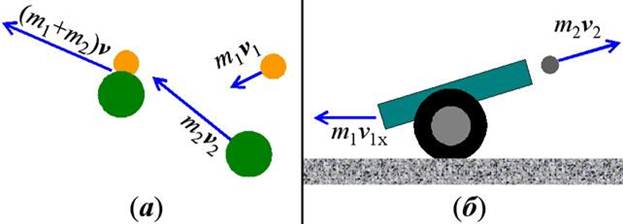
Рис. 14.(а) – к задаче о неупругом столкновении двух пластилиновых шаров; (б) – к вычислению скорости отдачи пушки после выстрела.
§ 15. РЕАКТИВНОЕ ДВИЖЕНИЕ: УРАВНЕНИЕ МЕЩЕРСКОГО, РАБОТЫ ЦИОЛКОВСКОГО И ОСВОЕНИЕ КОСМОСА