Взаимосвязь между константой химического равновесия и изобарно-изотермическим потенциалом.

При протекании реакции aA + bB = cC + dDдельтаG=cmC+dmD-amA-bmD . (2.29)

Поскольку химический потенциал любого компонента m i=mo+RT lnai, где Go - изменение изобарно-изотермического потенциала в случае, если реакция протекает при стандартном состоянии всех компонентов (ai = 1); Go== .При равновесии реакции G = 0. Поэтому это один из выводов закона действия масс. Так как при постоянной температуре Go - величина постоянная, то при равновесии отношение произведения активностей продуктов реакций, возведенных в степени, равные стехиометрическим коэффициентам, и произведению активностей исходных веществ - величина постоянная при постоянной температуре.Если равновесие реакции не достигнуто, где - фактическое отношение произведений активностей, когда равновесие реакции не достигнуто. Если активности всех компонентов стандартные (ai =1), то x0=1, lnx0=0 и уравнение (2.32) будет тождественным уравнению (2.31). Очевидно, что если фактическое отношение произведений активностей:

x0 = K; Go = 0 - равновесие реакции;

x0 < K; Go < 0 - протекает прямая реакция;

x0 > K; Go > 0 - протекает обратная реакция.

Во всех случаях необходимое термодинамическое условие протекания прямой реакции - уменьшение изобарно-изотермического потенциала (G < 0), называемого свободной энергией Гиббса.


26. Изменение энергии Гиббса как характеристика направления протекания химической реакции.

В химических процессах одновременно действуют два противоположных фактора — энтропийный и энтальпийный. Суммарный эффект этих противоположных факторов в процессах, протекающих при постоянном давлении и температуре, определяет изменение энергии Гиббса: то есть некоторое количество теплоты расходуется на увеличение энтропии, эта часть энергии потеряна для совершения полезной работы (рассеивается в окружающую среду в виде тепла), её часто называют связанной энергией. Другая часть теплоты может быть использована для совершения работы, поэтому энергию Гиббса часто называют также свободной энергией.

Характер изменения энергии Гиббса позволяет судить о принципиальной возможности осуществления процесса. При G<0 процесс может протекать, при G>0 процесс протекать не может (иными словами, если энергия Гиббса в исходном состоянии системы больше, чем в конечном, то процесс принципиально может протекать, если наоборот — то не может). Если же G=0, то система находится в состоянии химического равновесия.

Существует полезное соотношение, связывающее изменение свободной энергии Гиббса в ходе химической реакции с её константой равновесия : дельтаG=-RT*lnK. Вообще говоря, любая реакция может быть рассмотрена как обратимая (даже если на практике она таковой не является). При этом константа равновесия определяется как: K-k1/k-1.


27. Фазовые диаграммы и правило фаз.

Правило фаз. Фазовая диаграмма, количественно описывающая поведение гетерогенной системы, содержащей гомогенные области – фазы. Фазы отделены друг от друга заметными границами, которые называют поверхностями раздела. Каждая фаза гомогенна, однако она не непрерывна. Число фаз равно числу отделенных друг от друга структур, существующих в различных физических состояниях в системе. В одной системе могут существовать несколько жидких или твердых фаз, например: вода – масло, лед – твердая соль. Различают как число фаз, так и число компонентов, образующих фазу.Под числом компонентов понимают число независимых химических индивидуальностей.

Изучение гетерогенных систем сильно упростилось после предложенного в 1874 году Гиббсом обобщения, которое получило название «правило фаз». Оно состоит из очень простого соотношения: а = с – р + 2, где с – число компонентов системы, р – число фаз и f – число степеней свободы системы, т.е. число независимых переменных – таких, как температура, давление и концентрация, которые необходимы для полного описания системы. Согласно альтернативной формулировке правила фаз, число степеней свободы – это число независимых переменных, которые могут быть изменены без изменения числа фаз. Правило фаз применимо только для систем, находящихся в равновесии.

Посмотрим на фазовую диаграмму воды. Поскольку вода является единственным компонентом, значит с = 1. Вода существует в трех фазах – твердой, жидкой и газообразной. При этом число фаз, которые существуют в равновесии, зависит от температуры и давления.

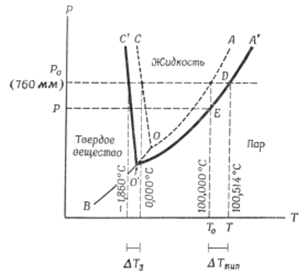
Рис. 6.1. Фазовая диаграмма воды и гипотетического 1 т идеального раствора (масштаб не соблюдается)

Линия ОА представляет собой кривую давления паров воды. Вдоль этой линии вода и пар находятся в равновесии друг с другом. Экспериментально такую линию получают путем измерения давления пара чистой воды при разных температурах.

Линия ОВ является кривой сублимации льда. Выше этой кривой вода существует в виде льда, ниже – в виде пара. В равновесии лед и пар находятся только вдоль линии ОВ, которая и является границей этих двух фаз.

Линия ОС описывает зависимость точки плавления льда от давления; лед и жидкая вода этой линии находятся в равновесии. Наклон линии ОС относительно оси ординат указывает на то, что при увеличении давления точка плавления льда понижается. Три кривые имеют общую точку пересечения 0, известную под названием «тройной точки».

Для зоны с = 1, р = 1 и f = 2. Для линий с = 1, р = 2 и f = 1. Для тройной точки с = 1, р = 3 и f = 0. Что означают различные степени свободы? То, что внутри зон f = 2, означает следующее: для описания поведения системы мы должны использовать и температуру и давление, т.е. обе величины могут меняться без изменения числа фаз, значит вода существует в жидком состоянии при различных температурах и давлениях. f = 1 означает, что мы можем установить точку на линии, т.е. описать систему только температурой или давлением. Т.е. вдоль линии каждой температуре соответствует строго определенное давление пара. При любом давлении пара для льда существует только одна точка для температуры плавления. В тройной точке система инвариантна, т.е. f = 0, т.е. система может находиться в равновесии только при одном значении температуры и давления.

Фазовая диаграмма (диаграмма состояния) — графическое отображение равновесного состояния бесконечной физико-химической системы при условиях, отвечающих координатам рассматриваемой точки на диаграмме (носит название фигуративной точки).


28. Уравнение Клаузиса-Клапейрона, 1-ое и 2-ое уравнения Рауля.

Объем, реально занимаемый одним молем растворенного вещества, называется парциальным молярным объемом растворенного вещества. Он соответствует изменению общего объема очень большого количества раствора при добавлении одного моля растворенного вещества. Очевидно, что при добавлении одного моля растворенного вещества концентрация не будет меняться только при условии бесконечно большого объема исходного раствора.В этом случае для парциального объема можно записать 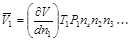,где V – общий объем раствора, Т – температура, Р –давление, n – число молей других веществ. Величина V является функцией Т и Р, а также состава раствора.

Закон Рауля. Точные измерения, которые позволили математически описать влияние растворенного вещества на физические свойства растворителя, были сделаны впервые Ф.-М. Раулем, работавшим в университете Гренобля в середине и конце XIX века (1830-1901 гг.).

Ф.-М. Рауль обнаружил, что давление пара раствора, содержащего нелетучее растворенное вещество, прямо пропорционально концентрации растворителя. Математически это можно записать так:

Р = kx1, где Р – давление пара раствора, k – константа пропорциональности, х1 – молярная доля растворителя. Когда растворенное вещество отсутствует х1= 1, то коэффициент k численно равен давлению пара чистого растворителя – Р0. Значит, Р = Р0х1. (6.11)

Поскольку х1+ х2= 1,0, где х2– молярная доля растворенного вещества, то мы можем преобразовать уравнение (6.11) в (6.12), подставив вместо х1 = 1 ‑ х2:

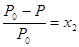. (6.12)

Это уравнение показывает, что относительное понижение пара растворителя равно мольной доле растворенного вещества и что давление пара раствора пропорционально молярной доле растворителя. Уравнения (6.11) и (6.12) отражают закон Рауля в преобразованной форме. Закон Рауля и уравнения (6.11) и (6.12) позволяют определить чистоту растворителя и наличие в нем нелетучих веществ.


29. Коллигативные свойства растворов (температура кипения, температура замерзания, осмотическое давление, давление насыщенного пара).

Рассмотрим, что происходит с растворителем, если в нем растворяют твердое вещество с исчезающе малым давлением пара. Некоторые свойства растворителя могут зависеть лишь от числа добавленных новых частиц. Интересно, что некоторые эти свойства мало зависят от природы растворенного вещества. Это происходит в том случае, если растворенное вещество не взаимодействует с растворителем и не подвергается ассоциации и диссоциации, т.е. число молекул сохраняется постоянным. В таком случае говорят о коллигативных растворах или о коллигативных свойствах растворов. Четыре свойства из группы коллигативных свойств обычно рассматриваются вместе: понижение давления пара, повышение точки кипения, понижение точки замерзания и осмотическое давление. Осмотическим давлением раствора называется то наименьшее давление, которое, помимо давления самого растворителя, необходимо приложить к раствору, чтобы предотвратить перетекание растворителя к раствору через мембрану, разделяющую раствор и растворитель, причем мембрана непроницаема для молекул растворенного вещества (полупроницаема) в направлении от чистого растворителя к раствору. Условием кристаллизации является равенство давления насыщенного пара растворителя над раствором давлению пара над твёрдым растворителем. Поскольку давление пара растворителя над раствором всегда ниже, чем над чистым растворителем, это равенство всегда будет достигаться при температуре более низкой, чем температура замерзания растворителя. Так, океанская вода начинает замерзать при температуре около минус 2 °C. Разность между температурой кристаллизации растворителя T°fr и температурой начала кристаллизации раствора Tfr есть понижение температуры кристаллизации. Понижение температуры кристаллизации бесконечно разбавленных растворов не зависит от природы растворённого вещества и прямо пропорционально моляльной концентрации раствора. Жидкость кипит при той температуре, при которой общее давление насыщенного пара становится равным внешнему давлению. Если растворённое вещество нелетучее (то есть давлением его насыщенных паров над раствором можно пренебречь), то общее давление насыщенного пара над раствором равно парциальному давлению паров растворителя. В этом случае давление насыщенных паров над раствором при любой температуре будет меньше, чем над чистым растворителем, и равенство его внешнему давлению будет достигаться при более высокой температуре. Таким образом, температура кипения раствора нелетучего вещества Tb всегда выше, чем температура кипения чистого растворителя при том же давлении T°b. Повышение температуры кипения бесконечно разбавленных растворов нелетучих веществ не зависит от природы растворённого вещества и прямо пропорционально моляльной концентрации раствора. Парциальное давление насыщенного пара компонента раствора прямо пропорционально его мольной доле в растворе, причем коэффициент пропорциональности равен давлению насыщенного пара над чистым компонентом.

 

30. Осмотический потенциал как основа пассивного транспорта.

Живым системам присущи различные физико-химические механизмы транспорта растворителя и растворенных веществ. Различают активный и пассивный транспорт. Активный транспорт характерен для живых мембран. Мы пока остановимся на пассивном транспорте, который более изучен и лучше может быть описан математически. Так, в 1748 году А. Ноллет впервые наблюдал, как растворитель проходит через мембрану из разбавленного раствора в более концентрированный. Если к более концентрированному раствору приложить давление, то в зависимости от его величины течение растворителя может быть замедлено, остановлено или обращено. Осмотическим давлением раствора называется то наименьшее давление, которое, помимо давления самого растворителя, необходимо приложить к раствору, чтобы предотвратить перетекание растворителя к раствору через мембрану, разделяющую раствор и растворитель, причем мембрана непроницаема для молекул растворенного вещества (полупроницаема) в направлении от чистого растворителя к раствору. Растворитель может перетекать из более разбавленного раствора в более концентрированный даже в том случае, если единственной разделяющей поверхностью между двумя растворами будет слой пара. По-видимому, осмотические эффекты не должны зависеть от природы мембран, используемых для их измерения. В противном случае можно бы было построить вечный двигатель, используя этот эффект.

31. Теория электролитической диссоциации Аррениуса.

1) при растворении в воде (или расплавлении) электролиты распадаются на положительно и отрицательно заряженные ионы (подвергаются электролитической диссоциации);2) под действием электрического тока катионы (+) двигаются к катоду (-), а анионы (-) – к аноду (+); 3) электролитическая диссоциация – процесс обратимый (обратная реакция называется моляризацией); 4) степень электролитической диссоциации α зависит от природы электролита и растворителя, температуры и концентрации. Она показывает отношение числа молекул, распавшихся на ионы (n), к общему числу молекул, введенных в раствор (N): Степень диссоциации слабого электролита можно связать с изотоническим коэффициентом. Будем считать, что из ^ N молекул электролита продиссоциировало n молекул, образовав νn ионов (ν – число ионов, на которое диссоциирует молекула). Поскольку изотонический коэффициент показывает, во сколько раз общее число молекул и ионов в растворе больше числа молекул до диссоциации, получаем: Соотношение (2.39) дает возможность, экспериментально определив изотонический коэффициент раствора, рассчитать степень диссоциации слабого электролита. Однако теория С. Аррениуса не учитывала всей сложности явлений в растворах. В частности, она рассматривала ионы как свободные, независимые от молекул растворителя частицы. Теории С. Аррениуса противостояла химическая, или гидратная, теория растворов Д.И. Менделеева, в основе которой лежало представление о взаимодействии растворенного вещества с растворителем. Кажущееся противоречие обеих теорий было устранено предположением о гидратации ионов (И.А. Каблуков).

32. Сильные и слабые электролиты. Особенности описания их свойств.

По способности к диссоциации электролиты разделяются на сильные и слабые. К сильным электролитам принадлежат сильные кислоты, сильные основания и большая часть солей. Большинство сильных электролитов кристаллизуются в кристаллах с ионной решеткой, и сильными электролитами часто называют только такие вещества. К слабым электролитам принадлежат в первую очередь слабые кислоты и слабые основания, а также некоторые соли. Сюда относятся большинство органических кислот, фенолы, амины, угольная и синильная кислота, а также такие соли, как хлорная ртуть, цианистая ртуть и др. Процесс диссоциации слабых электролитов является обратимым. Для электролита В2А диссоциация представляется уравнением: B2A « 2B+ + A2-.Как во всяком обратимом процессе, здесь устанавливается равновесие. Количественно его можно характеризовать константой равновесия (константой диссоциации Кд), определяемой для разбавленных растворов того же электролита В2А соотношением: 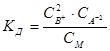, (7.1)

где СВ+, СА2-, См – концентрации соответствующих ионов и диссоциированных молекул электролита. Соотношение (7.1) применимо к слабым электролитам в разбавленных растворах; в более концентрированных растворах или в присутствии других электролитов в значительной концентрации необходимо пользоваться вместо концентрации активностями. В этом случае соотношение (7.1) приобретает вид: , (7.2)

где а2В+, аА2- и аМ – активность ионов и недиссоциированных молекул электролита. Напомним, что активностью (точнее термодинамической активностью) данного компонента называется такая величина, которая связана с другими термодинамическими величинами так же, как в идеальных растворах с ними связана концентрация этого компонента.

Коэффициент активности g равен отношению активности к концентрации.

Константу диссоциации, определяемую через активности по уравнению (7.2), называют термодинамической константой диссоциации. Практически, однако, при отсутствии данных об активности часто приходится и для срав­ни­тельно концентрированных растворов пользоваться соотношением (7.1).

Рассчитанную таким образом КД называют иногда условной константой диссоциации, поскольку она может несколько изменяться с концентрацией.

Изменение свободной энергии Гиббса в реакциях диссоциации при их выражении через активности выглядит следующим образом: 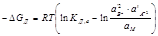. (7.3)

Оно зависит от состава раствора (концентрации данного электролита и других растворенных веществ раствора). Для стандартных условий
(a'В+ = а'А2- = a'M =1) тогда . (7.4)

Для характеристики состояния слабого электролита в растворе наряду с константой диссоциации пользуются также и величиной степени диссоциации a, которая определяется отношением: 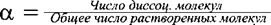. (7.5.)

Она зависит от следующих факторов:

· от природы растворителя и растворенного вещества;

· от температуры (с ростом Т растет и a );

· от концентрации раствора (с ростом С a уменьшается);

· от наличия одноименных ионов.