Квантовые ямы, проволоки и точки,

Квантовые яма – образец, один размер которого лежит в нанодиапазоне, а два других в микродиапазоне и выше. Пример (графен, монослой, нанослой на подложке, нанопленка).

Примером квантовой ямы является двумерная полупроводниковая структура состоящая из трех слоев. Пленка арсенида галлия 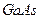нанометровой толщины с зоной (1,4 эв), окружена с обеих сторон слоями алюмината арсенида галлия с с более широкой запрещенной зоной(2 эв) при .В результате возникает профиль потенциальной энергии. близкий к по форме к прямоугольному с высотой барьера 0,4 эв для электронов и для дырок 0,2 эВ.

 

Рис.а)Прямоугольная потенциальная яма в трехслойной системе .

б)энергетические уровни.,в) энергетические подзоны.

 

 

Рис. Энергетическая диаграмма квантовой ямы.. а) в энергетическом пространстве,

б) в пространстве волновых векторов.

В направлении оси z движение электронов ограничено и квантуется, в плоскости остается свободным. Поэтому волновая функция электронов в квантовой яме принимает вид

Энергия электронов квантуется по оси :

. .

Где - ширина квантовой ямы

Квазинепрерывные значения волновых векторов определяются периодическими граничными условиями. , где -размер образца в плоскости.

Плотность состояний для двумерной электронной системы

в интервале электроны располагаются в подзоне с . В интервале электроны располагаются в двух подзонах и и плотность состояний удваивается. График полной плотности состояний в зависимости от роста энергии имеет ступенчатый характер с постоянной величиной ступеньки по оси ординат и энергии по оси абцисс. Ступенчатый характер функции подтверждается прямыми измерениями оптического поглощения.см рис мартин 133.+

 

Рис.Функция плотности состояний для двумерной электронной системы.

Квантовая проволока –образец, два размера которого лежат в нанодиапазоне и один в микродиапазоне и выше. пример (нанопроволока, молекула ДНК)

В квантовых проволоках электронный газ свободно движется по оси . По двум другим направлениям движение электронов ограничено и квантуется. Двумерное уравнение Шредингера имеет вид:

, где

Полная энергия электрона в квантовой проволоке для двумерного прямоугольного потенциала бесконечной длины следующая

.

В случае квантовых проволок энергетические уровни соответствующие поперечному движению описываются двумя квантовыми числами. Значения уровней энергии для электронных состояний возрастают при уменьшении толщины квантовых проволок.

Плотность состояний одномерного электронного газа

Представляется в виде узкого пика: слева это прямая , справа асимптота .

см рис. Учитывая, что получаем

где -групповая скорость

Электрический ток в одномерной системе .

 

Рис. Функция плотности состояний в зависимости от энергии для одномерной электронной системы. (квантовая проволока.)

Квантовая точка – это образец (нанокристаллл), все три размера которого лежат в нанодиапазоне. Пример (нанокластер). Примеры показаны на рис Пул199. Структуры получают нанолитографией. Реальные вантовые точки содержат большое число атомов до10⁴-10⁶. Энергетический спектр соответствует трехмерному потенциальному ящику.

Уравнение Шредингера имеет вид

Волновыми фикциями являются стоячие волны

и энергетические уровни

Функция плотности состояний квантовой точки представляет собой набор пиков дельта функций .Квантовой точке отвечает неэвидистантный дискретный спектр , атомной системе энергия . Плотность энергетических состояний для квантовых ям ,проволок и точек смна рис..

Квантовые точки создаются методом молекулярно-лучевой эпитаксии. Спонтанное формирование массивов вертикально связанных квантовых точек-нанкластеров осуществляется в режиме Странского –Крастанова. См в лекции мол.луч. эпитакс.

Метод самоорганизации квантовых точек на поверхности раздела двух материалов с разными параметрами кристаллической решетки. Материал выращивается химическим осаждением паров из газовой фазы на подложке из кристалла с большой постоянной кристаллической решетки и большой шириной запрещенной зоны 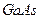. Возникающие пирамидки рассматриваются как примесные дефекты на поверхности основного полупроводника. Эти дефекты приводят к появлению электронных уровней ниже зоны проводимости и дырочных уровней энергии выше валентной зоны .см рис

Рис. экспериментальная полупроводниковая реализация квантовой точки в виде пирамидки на поверхности .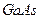

 

 

Рис. Зонная структура полупроводника содержащего квантовую точку.