Линейные множества
Непустое подмножество M(Ē) пространства En называется (вещественным) линейным подпространством(рис. 2.4), если оно удовлетворяет следующим двум условиям:
1) Если вектора xи y принадлежат M, тоx+y также принадлежит M.
2)Если произвольный вектор x принадлежит M, то lx при любом вещественном значении числа l также принадлежит M.
Из 2) видно, что если xÎM, то -xÎM. Тогда из 1) следует, что 0=x+(-x) также принадлежит M. Если мы осуществим смещение, определяемое фиксированным вектором x0 всех векторов непустого подпространства M пространства En, то получим подмножество называемое линейным многообразием (аффинным подпространством) пространства En. Оно не является линейным пространством, так как оно не содержит 0. Прямая в En, проходящая через начало, является одномерным пространством пространства En. Если сместить эту прямую, то мы получим линейное многообразие. Одно и тоже линейное многообразие может быть получено в результате смещений пространства M различными векторами.
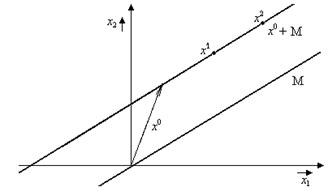
Рис. 2.4. Подпространство и линейное многообразие
Если максимальное число линейно независимых векторов, которые можно найти в M, равно r, то говорят, что M – r-мерное подпространство. Само пространство En можно рассмотреть как n– мерное пространство.
Гиперплоскостьюв En называется множество точек x, удовлетворяющих уравнению
Нab = {xÎEn|<a,x> = b}, (2.1)
где aÎEn, представляет собой вектор-нормаль к гиперплоскости, a¹ 0n, bÎE.
Обычно приставку гиперупотребляют для обозначения пространств, имеющих более чем три измерения. Гиперплоскость <a,x> = 0 содержит начало координат и является объединением всех прямых, которые проходят через начало координат и направляющие векторы которых ортогональны а,т.е. гиперплоскость есть множество точек, принадлежащим этим прямым
Гиперплоскость задает два замкнутых полупространства (рис. 2.5)
Н+ab = {xÎEn|<a,x>³ b}, Н-ab = {xÎEn|<a,x>£ b},
а также два открытых пространства
Н+ab = {xÎEn|<a,x>> b}, Н+ab = {xÎEn|<a,x> < b}.
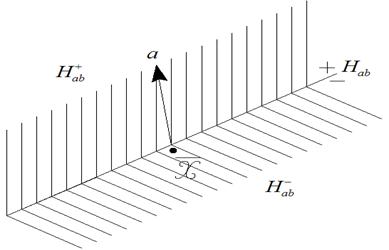
Рис. 2.5. К понятию полупространств
Вектор a, называемый нормалью к гиперплоскости Нab, к ней ортогонален и направлен в сторону полупространства Н+ab (рис. 2.5). Гиперплоскость Нab и соответствующие полупространства могут быть записаны с помощью некоторой фиксированной точки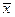 
ÎНab. При любом вещественном числе b уравнение <a,x> = b определяет линейное многообразие. Если задан некоторый вектор x0ÎEn такой, что <a,x0> = b, то линейное многообразие, определяемое уравнением <a,x> = b, можно рассматривать как смещение Нab на x0
В качестве примера рассмотрим гиперплоскость Н = {(x1, x2, x3, x4) | x1+x2-x3+2x4 = 4}. Нормалью к ней является вектор a= (1,1,-1,2)Т. Эта же гиперплоскость может быть записана с помощью любой другой точки из Нab, например с помощью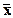 
= (0,6,0,-1)Т. В этом случае Нab = {(x1, x2, x3, x4)| x1+(x2-6)-x3+2(x4+1) = 0}.
Любую гиперплоскость в En можно задать в виде множества решений уравнения (2.1), подобрав соответствующим образом вектор a и число b.
Любую прямую в En можно задать в виде
{xÎEn| x= a+lc, lÎE} (2.2)
соответствующим образом, подобрав вектора a и c из En. Если в (2.2) число l ограничено сверху или снизу, то получаем луч. Если l ограничено сверху и снизу, то множество (2.2) задает отрезок.
Отрезком,соединяющим две данные точки x1, x2 в En называется множество таких точек, координаты xj которых связаны с координатами x1 и x2 соотношениями вида
{xjÎEn| xj=lxj1+(1-l)xj2, 0 £l £1, j = 1:n}.
Конкретный выбор l определяет положениеx на отрезке (при l = 1 точка xсовпадает с x1, при l = 0 – с x2, при 0<l<1 располагается между ними). Отношение, в котором находятся рассматриваемые x1, x2, x можно определить равенством
x= lx1+(1-l)x2 (0 £l £ 1).
Понятие «отрезок» тождественно понятию «замкнутый интервал» (рис 2.6).
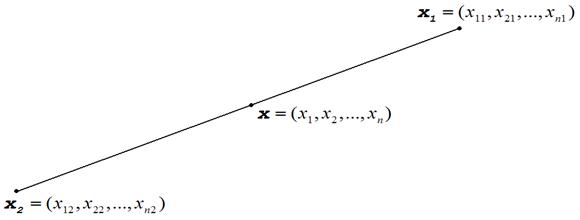
Рис. 2.6. К понятию отрезок (замкнутый интервал)