НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ (РАСПРЕДЕЛЕНИЕ ГАУССА)

Наибольшее распространение получил нормальный закон распределения, называемый часто распределением Гаусса:

(6.6)

где σ — параметр рассеивания распределения, равный СКО; Хц — центр распределения, равный МО.

 

Рис. 6.6. Экспоненциальные распределения

Широкое использование нормального распределения на практике объясняется центральной предельной теоремой теории вероятностей, утверждающей, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.

Вид экспоненциальных распределений при различных значениях показателя а приведен на рис. 6.6.

При введении новой переменной t = (х-Хц)/σ из (6.6) получается нормированное нормальное распределение, интегральная и дифференциальная функции которого соответственно равны:

Нормирование приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения интегральной и дифференциальной функций нормированного нормального распределения сведены в таблицы, которые можно найти в литературе по теории вероятностей.

Определенный интеграл с переменным верхним пределом

называют функцией Лапласа.

Равномерное распределение. Непрерывная случайная величина Х называется равномерно распределенной на отрезке 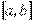(a<b), если ее функция плотности распределения (рис. 1.6, а) имеет вид :

Соответственно функция распределения на отрезке (рис. 1.6, б):

Рис. 1.6. Функции случайной величины, распределенной равномерно на [a,b]: а – плотности вероятностей f(x); б – распределения F(x)

Математическое ожидание и дисперсия данной СВ определяются выражениями:

, в силу симметрии функции плотности, совпадает с медианой. Моды равномерное распределение не имеет.

Показательное распределение. Распределение непрерывной случайной величины Х называется показательным (экспоненциальным), если плотность вероятности этой величины описывается функцией (рис. 1.7, а):

где λ – положительное число.

Соответственно функция распределения вероятностей имеет вид (рис. 1.7, б):

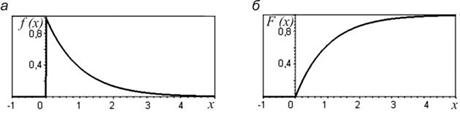
Рис. 1.7. Функции случайной величины, распределенной по показательному закону: а – плотности вероятностей f(x); б – распределения F(x)

Математическое ожидание и дисперсия равны соответственно

Распределение х² . Сумма квадратов стандартных нормальных случайных величин имеет распределение, которое называется х² -распределением с числом степеней свободы ν, равным числу независимых слагаемых в этой сумме [3]. Строгое определение требует указания плотности вероятности,

если

где 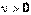– число степеней свободы (число независимых слагаемых в используемой в знаменателе суммы квадратов); – гамма-функция, то случайная величина (рис. 1.9). Однако эта формула не столь наглядна, как формулы для равномерного и нормального распределений. Важно знать информацию, указанную в начале этого пункта, а также следующее: максимум плотности вероятности при достигается при .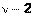

Рис. 1.9. Функции плотности вероятностей c2-распределения с числом степеней свободы: а – ν = 1; б – ν = 3; в – ν = 10

Математическое ожидание и дисперсия равны соответственно:

Распределение Стьюдента (t-распределение). Случайная величина в виде отношения двух независимых случайных величин и , , где , а , имеет распределение Стьюдента

(t-распределение) с числом степеней свободы . Функция плотности распределения имеет вид:

Математическое ожидание и дисперсия

Распределение Фишера (Фишера-Снедекора, распределение дисперсионного отношения, F-распределение). Случайная величина 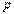в виде отношения двух независимых случайных величин, распределенных как (числитель) и (знаменатель), имеет F-распределение с числами степеней свободы и :

Иначе, случайная величина называется распределенной по F-распределению с параметрами 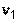и , если она имеет функцию плотности распределения

Математическое ожидание и дисперсия