Измерений. Лабораторная работа № 5
Ц е л ь р а б о т ы: изучение методик выполнения и обработки экспериментальных данных косвенных многократных и однократных измерений.
З а д а н и е н а р а б о т у:
1.Изучить теоретические материалы к лабораторной работе и материалы, приведенные на стр.42-45 данного практикума.
2. Экспериментальным путем определить, какие (однократные или многократные) измерения необходимо осуществлять при двух условиях работы объекта измерения.
3. Выполнить многократные косвенные измерения.
4.Выполнить однократные косвенные измерения.
5. Обработать полученные экспериментальные данные.
Т е о р е т и ч е с к и е о с н о в ы р а б о т ы
Обработка экспериментальных данных косвенных многократных измерений
Обработка экспериментальных данных косвенных многократных измерений базируется на использовании положений теории вероятностей и математической статистики о характеристиках функций случайных величин. В соответствии с этим положением оценкой истинного значения физической величины Y , определяемой как функция случайных величин (аргументов), может служить её значение  , полученное после выполнения вычислительных операций со средними арифметическими значениями
, полученное после выполнения вычислительных операций со средними арифметическими значениями 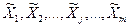 аргументов в соответствии с этой функцией:
аргументов в соответствии с этой функцией:
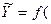 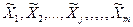 ) . ) .
| (3.13) |
Средние арифметические величин - аргументов определяются по формуле
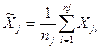 , ,
| (3.14) |
где nj - число измерений величины - аргумента Xj;
Xjl - значение величины Xj, полученное при выполнении l-го измерения.
Оценка среднеквадратического отклонения результата косвенного измерения определяется по формуле
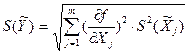 , ,
| (3.15) |
где S( 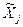 ) - оценка среднеквадратического отклонения результата измерений j-го аргумента, определяемое по формуле:
) - оценка среднеквадратического отклонения результата измерений j-го аргумента, определяемое по формуле:
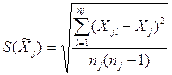 . .
| (3.16) |
Частные производные в формуле (3.15) принято называть коэффициентами влияния. Они вычисляются при значениях переменных, равных 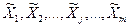 .
.
На основе формулы (3.15) получены формулы для определения погрешности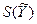 различных функциональных зависимостей, связывающих переменные при косвенных измерениях.
различных функциональных зависимостей, связывающих переменные при косвенных измерениях.
Так, например, для случая, когда при косвенном измерении используется функциональная зависимость
| Y = X1× X2 , | (3.17) |
оценка среднеквадратического отклонения результата косвенного измерения определяется по формуле:
 . .
| (3.18) |
В настоящее время в соответствии с принятыми в нашей стране методическими указаниями по обработке экспериментальных данных многократных косвенных измерений следует определять так называемую интервальную оценку (см. также стр.47-48) погрешности результата косвенного измерения. Для случая, когда результаты, полученные в процессепрямых измерений величин - аргументов, имеют нормальный закон распределения (при числе измерений 5 - 15 этот факт просто принимается), используется распределение Стьюдента (t - раcпределение), приведенное в приложении. Интервальная оценка определяется доверительной границей случайной погрешности результата косвенного измерения и вычисляется по формуле:
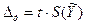 , ,
| (3.19) |
где t- коэффициент распределения Стьюдента.
Значение t определяется (см. приложение) в зависимости от принятого или заданного значения доверительной вероятности Рд (обычно Рд принимается равной 0.95) и найденного расчетным путем значения эффективного числа степеней свободы Кэфф, которое находят по формуле
Кэфф = 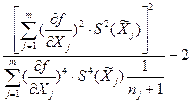 . .
| (3.20) |
Очевидно, что в случае, когда коэффициенты влияния 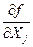 и число измерений nj для всех величин одинаковы, а также близки по модулям значения оценок среднеквадратических отклонений результатов измерений S(
и число измерений nj для всех величин одинаковы, а также близки по модулям значения оценок среднеквадратических отклонений результатов измерений S( 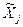 ), эффективное число степеней свободы Кэфф можно вычислить по формуле
), эффективное число степеней свободы Кэфф можно вычислить по формуле
| Кэфф = n - 1. | (3.21) |
Последовательность обработки экспериментальных данных косвенных многократных измерений при соблюдении условий, изложенных на стр.48 для прямых многократных измерений, приведена на рис.3.3.
| Получение результатов измерений величин X1,X2,...,Xj,...Xm | |
Вычисление средних арифметических 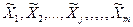 по формуле (3.14) по формуле (3.14)
| |
Вычисление значения  по формуле (3.13) по формуле (3.13)
| |
| Вычисление оценок среднеквадратических отклонений результатов измерений величин X1,X2,...,Xj,...Xm по формуле (3.16) | |
| Вычисление оценки среднеквадратического отклонения результата измерения величины Y по формуле (3.15) или (3.18) | |
| Вычисление числа степени свободы Кэфф по формуле (3.20) или (3.21) | |
| Принятие значения доверительной вероятности Рд (обычно Рд = 0.95) | |
| Определение коэффициента t в зависимости от Рд и Кэфф по таблице распределения Стьюдента | |
Определение доверительных границ 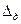 случайной погрешности по формуле (3.19) случайной погрешности по формуле (3.19)
| |
Запись результата измерений с использованием правил округления в виде: А =  ± ± 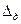 (Рд= ; Кэфф = ; n1= ; n2 = ; … ; nj = . ) (Рд= ; Кэфф = ; n1= ; n2 = ; … ; nj = . )
|
Рис. 3.3
Обработка экспериментальных данных косвенных однократных измерений.
Однократные косвенные измерения проводятся при условиях, когда всеми погрешностями кроме погрешностей средств измерений можно пренебречь. Оценка значения измеряемой величины при однократных косвенных измерениях находится из выражения:
 , ,
| (3.22) |
где  - значения физических величин - аргументов, найденные по шкалам соответствующих измерительных приборов.
- значения физических величин - аргументов, найденные по шкалам соответствующих измерительных приборов.
Результаты измерений записываются в виде:
А = 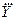 ± D , ± D ,
| (3.23) |
где D - оценка погрешностей косвенных однократных измерений.
При определении оценки погрешности косвенных однократных измерений считают, что погрешности измерений величин - аргументов являются случайными, имеющими равномерный закон распределения. На этом основании для определения D используют формулу (3.15), в которой вместо значенияS( 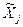 ) подставляют абсолютные погрешности измеренийD(
) подставляют абсолютные погрешности измеренийD( 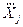 ) величин - аргументов.
) величин - аргументов.
Например, для случая когда при косвенных измерениях используются функции вида (3.17), погрешность косвенных однократных измерений определяется из выражения:
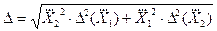 . .
| (3.24) |
Для определения значений D( 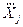 ) необходимо использовать информацию о классах точности применяемых средств измерений.
) необходимо использовать информацию о классах точности применяемых средств измерений.
В подавляющем большинстве случаев класс точности нормируется приведенной g или относительной d погрешностью.
L = g =  , ,
| (3.25) |
L = d =  , ,
| (3.26) |
где Xв и Xн - верхний и нижний пределы измерений используемого средства измерений.
Значение класса точности указывается на шкалах или корпусах измерительных устройств. При этом, если число, определяющее класс точности заключено в окружность-‚, то класс точности устройства следует определять по формуле (3.26), в противном случае - по формуле (3.25).
Таким образом, в каждом конкретном случае для определения значений D( 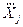 ) необходимо выполнять вычисления по формулам, полученным из выражений (3.25) и (3.26):
) необходимо выполнять вычисления по формулам, полученным из выражений (3.25) и (3.26):
D( 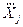 ) = ) = 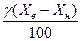 , ,
| (3.27) |
D( 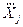 ) = ) = 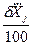 . .
| (3.28) |
О п и с а н и е л а б о р а т о р н о г о с т е н д а
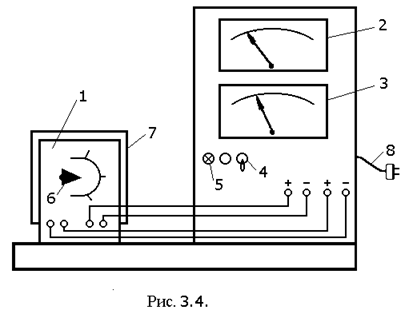
Лабораторный стенд (рис.3.4) содержит миниатюрную электрическую печь 1, вольтметр 2, амперметр 3, тумблер 4, сигнальную лампу 5, переключатель режимов работы печи 6, защитный кожух 7 и вилку 8.
Вольтметр и амперметр включены в соответствующие цепи питания электрической печи и служат для измерений напряжений и тока питания печи. Переключатель 6 обеспечивает работу печи в трех различных по потребляемой электрической мощности режимах, а защитный кожух 7 позволяет изолировать печь от внешних возмущающих воздействий.
|
П о р я д о к в ы п о л н е н и я р а б о т ы
Сущность экспериментов в данной лабораторной работе сводится к выполнению многократных и однократных измерений мощности, потребляемой электрической печью в одном из трех (по указанию преподавателя) режимах. В данных косвенных измерениях используется функциональная зависимость между мощностью W, напряжением U и током I:
| W = U× I . | (3.29) |
1.С помощью вилки 8 включить стенд в электричекую сеть, тумблер 4 установить в положение "Вкл.". При этом должна загореться сигнальная лампа 5.
2.Снять защитный кожух 7. Переключатель 6 установить в положение Р1(1-й режим работы печи).
3.Выждать 10 минут и приступить к выполнению многократных косвенных измерений, считывая показания вольтметра и амперметра через каждые 15 с. Выполнить 13 - 15 отсчетов, а результаты измерений записать в таблицу 3.4.
4.Операций по п. 3 выполнить для режима 2 и режима 3 электрической печи, устанавливая последовательно переключатель 6 в положениеР2 и Р3.
5.Надеть на печь защитный кожух7.
6.Выждать 5 мин, удостовериться в том, что показания вольтметра и амперметра перестали изменяться во всех режимах работы печи, и выполнить однократные косвенные измерения, считав показания вольтметра и амперметра для всех 3-х режимов работы электрической печи.
7.Выключить тумблер 4, а вилку 8 отключить от электрической печи.
8.Для каждого режима работы печи по результатам многократных косвенных измерений определить максимальные, минимальные значения напряжения, тока и разности этих значений. Результаты занести в таблицу 3.4.
9.Сделать вывод о диффузионности измеряемых напряжений и токов.
10.Для одного из режимов работы печи (по указанию преподавателя), выполнить обработку экспериментальных данных многократных и однократных косвенных измерений, используя приведенные выше методики. Результаты занести в таблицы 3.5 и 3.6.
Таблица 3.4
| № п.п. | Режим 1 | Режим 2 | Режим 3 | ||||
| U, В | I, А | U, В | I, А | U, В | I, А | ||
| Многократные измерения | |||||||
| ... | |||||||
| Максимальные значения Uмакс, Iмакс | |||||||
| Минимальные значения Uмин, Iмин | |||||||
| Разность Uмакс-Uмин, Iмакс-Iмин | |||||||
| Однократные измерения | |||||||
Таблица 3.5
| № п.п. | Результа- ты отдельных измерений | Оценки | Кэфф | t | Dд, Вт | Результат А, Вт | ||||||
| U,В | I,А | 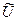 , В , В
| 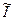 ,А ,А
| S( 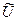 )В )В
| S( 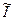 )
А )
А
|  ,
Вт ,
Вт
| S(  ),
Вт ),
Вт
| |||||
Таблица 3.6
| Показания приборов | Оценки | Результат А, Вт | ||||
 , В , В
| 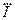 , А , А
| 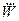 , Вт , Вт
| 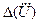 , В , В
| 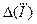 , А , А
| D, Вт | |
При обработке экспериментальных данных по формулам принять X1=U, X2=I.