Импульсные и цифровые САУ
Дискретные САУ
Импульсные системы – это системы, в которых действуют сигналы квантованные по времени. Импульсный элемент осуществляет квантование непрерывного сигнала x(t) по времени, преобразуя его в дискретный сигнал x*(t). Квантование называют импульсной модуляцией, которая заключается в изменении одного из параметров выходных импульсов (модулируемого параметра) в функции величины входного (модулирующего) сигнала. Модулируемым параметром для последовательности импульсов на выходе импульсного элемента (ИЭ) может быть высота (амплитуда) импульса, его ширина или пауза между импульсами. Соответственно существуют три вида импульсной модуляции: амплитудно-импульсная модуляция (АИМ), широтно-импульсная модуляция (ШИМ) и время-импульсная модуляция (ВИМ). Последняя подразделяется на фазо-импульсную модуляцию (ФИМ) и частотно-импульсную модуляцию (ЧИМ). Во всех случаях форма импульсов принимается неизменной.
При АИМ модулируемым параметром, зависящим от значения входного сигнала ИЭ x(t) в начале очередного периода Т0 повторения импульсов, является высота (амплитуда) импульсов А.
При ШИМ модулируемым параметром является ширина импульса Тn при постоянном периоде Т0 повторения импульсов.
При ФИМ модулируемым параметром является запаздывание tзап относительно начала периодов при постоянном Т0.
При ЧИМ – модулируемым параметром является частота ln 
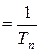следования импульсов, изменяющаяся в зависимости от x(t).
Соответственно по виду модуляции системы с АИМ относят к классу линейных дискретных систем и с ШИМ, если пренебречь эффектом квантования по уровню. Эти системы получили наибольшее распространение.
Основное достоинство дискретных систем:
а) возможность многоточечного (многоканального) управления;
б) многократное использование линий связи;
в) повышенная помехозащищенность.
Первое достоинство заключается в том, что с помощью одного управляющего устройства (УУ) можно управлять несколькими объектами путем циклического подключения УУ последовательно к каждому УО. Система управления существенно упрощается по сравнению со случаем применения УУ для каждого объекта.
Возможность многократного использования одного канала связи для управления несколькими объектами, удаленными от места расположения УУ основана на том же принципе последовательного подключения объектов и соответствующих УУ линий связи с помощью синхронно действующих на обоих концах линий связи (шаговых) распределителей. Это временное разделение каналов.
Повышенная помехозащищенность обусловлена возможностью передавать информацию в виде очень коротких импульсов, в промежутке между которыми система оказывается разомкнутой и не реагирует на внешние возмущения.
Линейная система импульсного регулирования
Линейной системой импульсного регулирования называется такая система автоматического регулирования (САР), которая кроме звеньев непрерывного действия содержит импульсное звено, преобразующее непрерывный сигнал в равноотстоящие друг от друга импульсы.
Варианты выходных последовательностей импульсных звеньев (рис. 1).
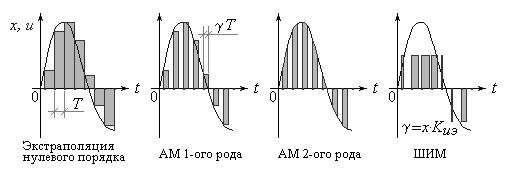
Рисунок 1 – Выход импульсного звена
Математический аппарат описания импульсных систем
Непрерывная функция 
может быть представлена решетчатой функцией 
.
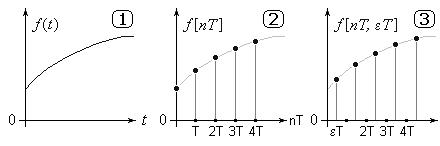
Рисунок 3 – Решетчатые функции
Решетчатые функции 2 определены только в дискретные моменты времени [nT] (сокращенно [n]) и формируются из непрерывных функций 1: f [nT] = f (t) при t=nT. Рассматривают также смещенные решетчатые функции (последовательность 3): f [n,ε] = f (t) при t=(n+ε)T, где ε-относительное смещение, 
.
- безразмерное время; 
.
Непрерывные функции, проходящие через дискреты заданной решетчатой функции, называют огибающими. Их бесконечно много.
Рисунок 4 – Синтез огибающих
Основная огибающая может быть получена, как результат решения ДУ наименьшего порядка и должна содержать гармоники наименьшей частоты.
Для решетчатых функций времени вводится понятие дискретного преобразования Лапласа.
, (1)
где 
- решетчатая функция (n=1,2,3…);
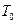- период повторения дискретных значений решетчатой функции;
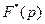- дискретное изображение функции ;
- символ дискретного преобразования.
Для решетчатой функции в относительном времени 
, формула дискретного преобразования принимает вид:
, (2)
где 
- новая безразмерная комплексная переменная, 
; 
- относительная частота 
; 
- абсцисса сходимости ряда.
Введем обозначение 
, и тогда выражение (1) примет вид:
(3)
и соответствует 
-преобразованию дискретного сигнала, - символ этого преобразования.
Правила преобразования структурных схем дискретных систем
Рисунок 7 – Соединение звеньев
1. 
.
2. 
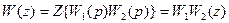, т.е. 
.
3. 
.
Структура импульсной системы
Для определения устойчивости и расчета переходной характеристики надо записать передаточную функцию приведенной непрерывной части системы, которая включает непрерывную часть и формирователь импульсов (в импульсной системе) или ЦАП (экстраполятор нулевого порядка) – в цифровой.
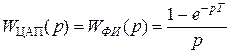- в изображениях Лапласа,
Т – период дискретности.
, 
,
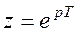
где H(p) – изображение Лапласа переходной функции. Следовательно, можно найти h(t) по H(p) – изображению, а затем найти z-преобразование для функции времени. Можно найти таблицы перехода от H(p) к z-преобразованию, т.е. H(z), не находя h(t).
Например, раскладываем на простые слагаемые:
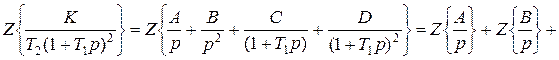
Коэффициенты A, B, C, D – определяются приравниванием числителя и коэффициента К.
Найдя передаточную функцию приведенной непрерывной части в z-форме, нужно найти z-передаточную функцию системы в замкнутом состоянии.
Тогда z-изображение переходной функции равно произведению WЗАМ(z) на z-изображение 1-ой ступенчатой функции, т.е. 1(t) ®x(t)
По характеристическому уравнению в z-форме можно оценить устойчивость.
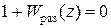
Все корни z-уравнения по модулю должны быть меньше единицы в устойчивой системе.
Переход оси z-изображения переходной функции к оригиналу h(nT), t=nT – дискретное время, выполняется по обратному преобразованию (g - интегрирование вдоль окружности единичного радиуса r)
Найти ординаты h(t) в дискретные моменты можно делением полинома числителя H(z) на полином знаменателя. Конечное значение h[nT]|h®: можно определить, используя теорему о пределах:
Если система устойчива, предел существует.
Например, для структурной схемы:
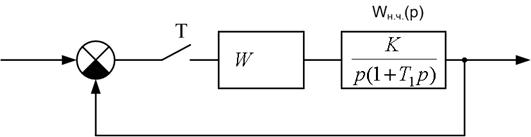
; z=epT;
По таблицам переходим от преобразования Лапласа к z-преобразованию.
Обозначим 
Найдем Wзам:
Запишем изображение переходной характеристики:
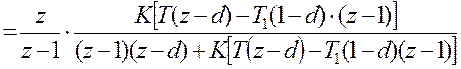
Пусть К=2, Т1=1с, Т=0,1с.
.
е-0,1=0,9048, тогда
Характеристическое уравнение системы:
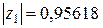
Корни по модулю меньше единицы – система устойчива.
h[nT] – получаем делением полинома числителя H(z) на полином знаменателя, записав изображение для отрицательных степеней z (т.е. поделив почленно числитель и знаменатель на z2).
Результаты деления дают ординаты переходной характеристики в дискретные моменты (n – определяет степень при z)
| h | … | : | ||||
| h[nT] | 0,0096 | 0,027 | 0,0436 | 0,057 | ... |
Время счета – дискретное –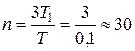 
Рисунок 43.
Приложение – Таблица z-преобразований
| F(p) | f(t) | F(z) |
| 
| 
|
| 
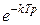
| 1 или 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|