Бинарные деревья

 

D = (либо пусто, либо D^о);

D^о = (i:инф; лев:D; прав:D).

Операции:

· Создать (Создается пустое дерево)

· Пусто? (Функция логического типа, истина, если дерево пусто, ложь в противном случае)

· Корень? (Функция логического типа, истина, если дерево состоит лишь из корня. Такое дерево можно назвать «пнем»)

· Корень (Процедура выделяет из дерева корень, левое и правое поддеревья как самостоятельные деревья)

· Левое поддерево (Процедура выделяет из дерева левое поддерево, корень, и правое поддерево как самостоятельные деревья)

· Правое поддерево (Процедура выделяет из дерева правое поддерево, корень и левое поддерево как самостоятельные деревья)

· Конструирование (Из «пня» и двух деревьев конструируется дерево. Это операция, обратная к предыдущим трем)

· Обходы (6 штук! Их названия – ЛКП, ЛПК, ПКЛ, ПЛК, КЛП, КПЛ зависят от порядка обхода)

 

Пример.Правильное арифметическое выражение (((a+b)*c)/(c+d)).

Представим в виде бинарного дерева

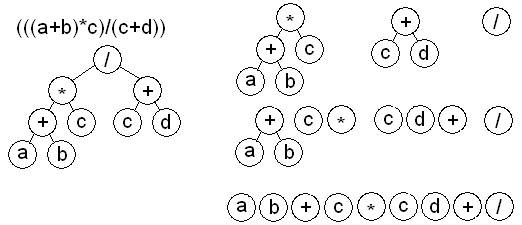
Обходы:

ЛКП – (((a+b)*c)/(c+d)) – исходное выражение.

ЛПК – ab+c*cd+/ – обратная польская запись.