Специальные задачи линейного программирования: задача о назначениях, решение средствами MS Excel

Задача о назначениях является частным случаем транспортной задачи, в котором все значения a_i и b_j равны 1. Такая задача возникает при распределении людей на должности или работы, водителей на машины, рабочих на станки, автомашин на маршруты, групп по аудиториям и т.п.

Постановка задачи(об оптимальном закреплении исполнителей на работы). Имеется n видов работ и n исполнителей этих работ. Известна эффективность c_ij выполнения исполнителем i работы j. Требуется так назначить исполнителей по видам работ, чтобы суммарный эффект от назначений был максимальным.

Часто исходные данные задачи о назначениях записывают в виде таблицы (матрицы) планирования:

Работы Исполнители	B1	B2	¼	Bn	Число исполнителей
A1	c11	c12	¼	c1n
A2	c21	c22	¼	c2n
¼	¼	¼	¼	¼	¼
An	cn1	cn2	¼	cnn
Количество работ			¼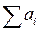

Составим экономико-математическую модель (задача о назначениях относится к двухиндексным задачам линейного программирования):

1) вводим переменны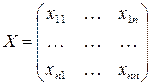е: , где

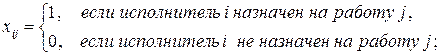
2) задаем целевую функцию , которая выражает суммарный эффект от назначений;

3) из условий задачи составляем ограничения:

a) каждый исполнитель должен быть назначен на работу, т.е.

;

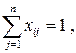
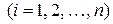b) на каждую работу должен быть назначен исполнитель, т.е.

.

Таким образом, модель задачи о назначениях имеет следующий вид:

Найти минимальное значение целевой функции
	(11.1)
при ограничениях
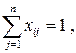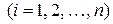,	(11.2)
,	(11.3)
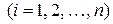, , .	(11.4)

Замечание. Если число исполнителей m не равно числу работ n (т.е. задача является открытой), то возможно применение двух способов:

1) решение открытой задачи о назначениях сводим к решению закрытой задачи о назначениях; для этого вводим фиктивных исполнителей или фиктивные виды работ;

2) изменяем ограничения 11.2 и 11.3:

a) если число исполнителей m больше числа работ n, то

; ;

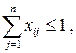
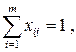
b) если число исполнителей m меньше числа работ n, то

; .
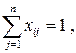