Специальные задачи линейного программирования: транспортная задача, решение средствами MS Excel

Транспортная задача является одной из наиболее распространенных задач линейного программирования и находит широкое практическое приложение.

Постановка задачи(об оптимальном закреплении потребителей к поставщикам). Некоторый однородный продукт, сосредоточенный у m производителей (поставщиков) A_i в количестве a_i единиц, необходимо доставить n потребителям B_j в количестве b_j единиц. Известна стоимость c_ij перевозки единицы груза от поставщика i к потребителю j. Необходимо составить план перевозок, позволяющий с минимальными затратами перевезти все грузы и полностью удовлетворить потребителей.

Часто исходные данные транспортной задачи записывают в виде таблицы (матрицы) планирования:

Потребитель Производитель	B₁	B₂	¼	B_n	Предложение (запасы)
A₁	c₁₁	c₁₂	¼	c₁_n	a₁
A₂	c₂₁	c₂₂	¼	c_2n	a₂
¼	¼	¼	¼	¼	¼
A_m	c_m₁	c_m2	¼	c_mn	a_m
Потребность (спрос)	b₁	b₂	¼	b_n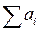

Составим экономико-математическую модель (транспортная задача относится к двухиндексным задачам линейного программирования):

1) вводим переменные: , где x_ij – количество единиц груза, перевозимых от поставщика i к потребителю j ; стоимость этой перевозки составит ;

2) задаем целевую функцию , которая выражает стоимость перевозок всех грузов;

3) из условий задачи составляем ограничения:

a) все грузы должны быть перевезены, т.е.

;

b) все потребности должны быть удовлетворены, т.е.

Таким образом, модель транспортной задачи имеет следующий вид:

Найти минимальное значение целевой функции
	(10.1)
при ограничениях
,	(10.2)
,	(10.3)
, , .	(10.4)

В рассмотренной модели предполагается, что суммарные запасы равны суммарным потребностям, т.е.

(10.5)

Транспортная задача, в которой суммарные запасы и суммарные потребности совпадают, называется закрытой транспортной задачей, в противном случае получаем открытую транспортную задачу.

Замечание. Решение открытой ТЗ проводится сведением к закрытой ТЗ (введением фиктивного поставщика или фиктивного потребителя):

a) если суммарные запасы превышают суммарные потребности, то вводится фиктивный потребитель B_n₊₁, потребность которого равна ;

b) если суммарные потребности превышают суммарные запасы, то вводится фиктивный поставщик A_m₊₁, запасы которого равны .

Стоимость перевозки единицы груза до фиктивного потребителя или от фиктивного поставщика приравнивается нулю, так как груз в обоих случаях фактически не перевозится.