Классическая задача оптимизации, решение методом множителей Лагранжа

Если в задаче оптимизации отсутствует условие неотрицательности переменных, а функциональные ограничения имеют вид равенств, то такую задачу называют классической задачей оптимизации:

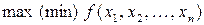
	(4.1)
.	(4.2)

Если все функции 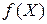, 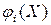непрерывны вместе с частными производными первого порядка, то для решения задачи оптимизации можно применить классический метод множителей Лагранжа.

Алгоритм:

1. Сначала составляют функцию Лагранжа:

.

(4.3)

2. Далее вычисляют для функции (4.3) частные производные первого порядка по всем переменным 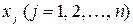и 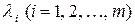, приравнивают их нулю и получают систему уравнений:

(4.4)

3. Если удается найти все решения системы (4.4), то для определения глобального максимума или минимума достаточно найти значения функции в соответствующих точках области определения задачи и выбрать наибольшее или наименьшее значение функции.

Замечание. Теоретической основой метода является следующее утверждение:

если функция f(X) в точке 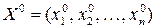имеет экстремум, то существует вектор 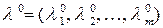такой, что точка 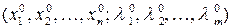является решением системы уравнений (4.4).