Общая классификация. Примеры практических приложений

Определение 1.Задача оптимального программирования имеет вид:

Найти максимум или минимум функции
	(3.1)
при ограничениях
	(3.2)
	(3.3)

f(X) – целевая функция (ЦФ), зависящая от вектора X;

Обозначение говорит о том, что в каждом конкретном ограничении возможен один из этих знаков. Ограничения (3.1) называются функциональными ограничениями, а (3.2) – прямыми ограничениями.

Более компактно:

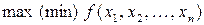
	(3.4)
	(3.5)
	(3.6)

Вектор X называется допустимым решением (допустимым планом задачи оптимального программирования), если его компоненты 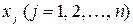удовлетворяют системе ограничений (3.4) и (3.5).

План называется оптимальным планом задачи оптимального программирования, если .

Определение 2.Решить задачу оптимального программирования – это значит:

1) найти оптимальный план ;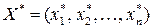

2) найти оптимальное значение .

Задачи оптимального программирования классифицируют по следующим признакам:

· линейные и нелинейные задачи (по характеру связей между переменными);

· непрерывные и дискретные задачи (по характеру изменения переменных);

· статические и динамические задачи (по учету фактора времени);

· однокритериальные и многокритериальные задачи (по числу критериев оценки альтернатив);

· задачи в условиях полной определенности, в условиях неполной информации (случай риска) и в условиях неопределенности (по наличию информации о переменных).