Решение уравнений с двумя переменными
как квадратных относительно одной из переменных
При решении уравнений методом сведения к квадратному уравнению необходимо рассмотреть и оценить дискриминанты этих уравнений.
Задача 1. Решите в целых числах  .
.
Решение. Если попытаться решить данное уравнение методом разложения на множители, то это достаточно трудоемкая работа, поэтому это уравнение можно решить более изящным методом. Рассмотрим уравнение как квадратное относительно  :
:  . Корни данного уравнения
. Корни данного уравнения  .
.
Данное уравнение имеет решение тогда и только тогда, когда дискриминант этого уравнения равен нулю, т. е.  , отсюда
, отсюда  . Если
. Если  , то
, то  .
.
Ответ:  .
.
Обобщение: Эту и последующие задачи можно привести к общему виду  (1) или
(1) или  (2) где
(2) где  - любые выражения, а именно: в (1) выражения
- любые выражения, а именно: в (1) выражения  зависят от
зависят от 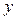 , в (2) – зависят от
, в (2) – зависят от  .
.
Например, 
Задача 2. Решите в натуральных числах  .
.
Решение. Перепишем уравнение в виде 
 . Данное уравнение является квадратным относительно переменной
. Данное уравнение является квадратным относительно переменной  , тогда
, тогда 
 . Уравнение имеет корни, если
. Уравнение имеет корни, если  , т.е.
, т.е.  . Отсюда
. Отсюда  (*).
(*).
Так как  , то условию (*) не удовлетворяет ни одно значение
, то условию (*) не удовлетворяет ни одно значение  . Значит, решений в натуральных числах нет.
. Значит, решений в натуральных числах нет.
Ответ: решений в натуральных числах нет.
Задача 3. Решите уравнение  .
.
Решение. Рассмотрим данное уравнение как квадратное относительно  с коэффициентами, зависящими от
с коэффициентами, зависящими от 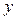 ,
, 

Найдем четверть дискриминанта 
 Отсюда следует, что уравнение имеет решение только тогда, когда
Отсюда следует, что уравнение имеет решение только тогда, когда  = 0, отсюда следует
= 0, отсюда следует  , затем находим
, затем находим  .
.
Ответ:  .
.
Задача 4. Решите в целых числах 
 .
.
Решение. Запишем уравнение в виде 
 ,
,  .
.
Решаем это уравнение относительно  :
:  .
.
Так как  - целое число, то
- целое число, то  должно быть целым числом. Значит, дискриминант уравнения должен быть квадратом целого числа, т. е.
должно быть целым числом. Значит, дискриминант уравнения должен быть квадратом целого числа, т. е.  , где
, где  ,
,
 (*)
(*)
 (**)
(**)
Из равенств (*) и (**) следует, что 

 .
.
Видно, что при любом  и
и  .
.
Ответ: 


 где
где 
Это решение показывает, что уравнения можно рассматривать как квадратные не только относительно одной из своих переменных, но и относительно какого-либо выражения.
Творческое задание: Сконструировать авторские задачи по данной теме.