Вычисление тензоров инерции некоторых тел
Центральный тензор инерции шара – шаровой: 
, тензоры инерции цилиндра и конуса трансверсально–изотропные: 
, что позволяет свести трехмерные интегралы к одномерным.
Шаровой слой(рис. 5.10,a).Центральный тензор инерции – шаровой: 
. Складывая моменты инерции, получим:
.
Объем слоя 
. В качестве элемента массы 
возьмем массу шарового слоя толщиной 
: 
, где плотность 
, а элементарный объем 
.
Тогда 
и окончательно 
Рассмотрим частные случаи:
а) шар ( 
: 
;
| Рис. 5.10. Шар, цилиндр, конус |
|
| б) |
| r |
| dr |
|
| a) |
| R |
| в) |
| R |
| r |
|
|
|
|
| · C |
| A · |
б) оболочка (
: 
.
Полый прямой круговой цилиндр (рис. 5.10,б).
Найдем сначала 
.Выделим двумя цилиндрическими поверхностями радиуса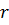 
и 
трубку толщиной и от тройного интеграла перейдем к одинарному:
.
Учитывая, что 
, найдем сумму:
.
Разделив цилиндр на пластинки толщиной 
и массой 
, найдем
.
Итак, 
, 
.
Рассмотрим частные случаи:
а) сплошной цилиндр 
, 
;
б) оболочка ( 
): 
, 
;
в) пластинка ( 
): , 
;
г) стержень ( 
): 
, 
.
Прямой круговой конус(рис. 5.10,в).
Радиус основания R, высота h, плотность 
.
Найдем 
. Чтобы не вычислять тройной интеграл по ( 
) в декартовых координатах (или по 
в цилиндрических), разобьем конус на пластинки толщиной , радиусом 
и с моментом инерции
. Тогда 
.
Найдем сумму 
и, вычислив интеграл 
,получим:
.
Моменты инерции относительно центральных осей вычисляются с помощью теоремы Гюйгенса – Штейнера ( 
):
