Алгоритм абстрактілі машина іспеттес.
Тьюринг машинасы – белгілі бір есептерді шығаруға арналған қатаң математикалық құрылым, математикалық аппарат. Бұл аппарат машина деп аталу себебі оның құрамдас бөлігінің және функцияларының есептеу техникасына ұқсауында. Тьюринг машинасының есептеу техникасынан ерекшелігі оның еске сақтау құрылғысы шексіз лентадан тұруында, ал есептеу техникасының еске сақтау құрылғысы қаншалықты үлкен көлемді болса да шектеулі. Сондықтан Тьюринг машинасын лентасы шексіз болғандықтан есептеу техникасы түрінде қолдануға болмайды.
Тьюринг машинасымен жұмыс істеу үшін объектілер туралы ұғымдарға тоқталу қажет.
Анықтама. Әлдебір алфавиттен алынған әріптердің кез келген тізбегі осы алфавитте сөз деп аталады.
Анықтама. Сөздегі әріптердің саны сөз ұзындығы деп аталады. Әріптері жоқ сөзді бос сөз дейді. Олар «  » немесе
» немесе  деп белгіленеді.
деп белгіленеді.
Әлемдегі барлық объектілерді әртүрлі алфавиттегі сөздер түрінде қарастыруға болады. Сондықтан алгоритмнің жұмыс істеу объектілері сөздер болып табылады.
Анықтама. Алгоритм қолданылатын сөзді енгізілетін сөз дейді. Алгоритмнің нәтижесі шығарылатын сөз деп аталады. Алгоритм қолданылатын сөздердің жиыны алгоритмнің қолданылу облысы деп аталады.
Әрбір Тьюринг машинасында 2 бөлік бар:
1. Ұяшықтарға бөлінген екі жағынан да шексіз лента
2. Автомат - жазу/оқу инесі
Тьюринг тезисі: Кез келген алгоритм үшін сәйкес Тьюринг машинасын құруға болады.
Анықтама. Тьюринг машинасы деп  жүйесін айтады. Мұндағы: А – шекті –жиын, Тьюринг машинасының алфавиті,
жүйесін айтады. Мұндағы: А – шекті –жиын, Тьюринг машинасының алфавиті,  - А алфавитінің бос сөзі, Q –Тьюринг машинасының жағдайын білдіретін шекті жиынның элементі, q1- ТМ-ның бастапқы жағдайы, q0- МТ-ның тоқтау жағдайы, пассивті жағдай, Т-МТ-ның жылжу жиыны,
- А алфавитінің бос сөзі, Q –Тьюринг машинасының жағдайын білдіретін шекті жиынның элементі, q1- ТМ-ның бастапқы жағдайы, q0- МТ-ның тоқтау жағдайы, пассивті жағдай, Т-МТ-ның жылжу жиыны,  - МТ-ның программасы.
- МТ-ның программасы.
Анықтама. Алгоритм (Тьюринг бойынша) – қойылған есепті шешуге келтірілетін Тьюринг машинасына құрылған программа.
Тьюринг машинасы мен тезисі болашақта да қолданылады, себебі кез келген проблема шешілмейді деп айтуға болмайды, шешілмейтін есеп болмауы керек, оны қандай да бір шешілетін түрге келтіру керек, соған орайластырылған алгоритм құрастыру керек.
Машинаның белгілі бір процесті орындауының өзі алгоритмдік процесс болып табылады. Сондықтан алгоритмге қойылатын талаптар мен қасиеттер оны орындайтын машинаға да қойылады:
1) Машинаның жұмысы дискретті, бірінен кейін бірі орындалатын жеке – жеке командалармен орындалуы керек.
2) Әрекеттер детерминделген , яғни қадамдар қатаң реттелген , ал олардың нәтижесі алдыңғы қадамда алынған нәтижелермен тікелей байланысты болуы керек.
3) Жұмыс алдында алғашқы берілгендер алгоритмнің анықталу облысынан алынуы керек.
4) Саны санаулы қадамдарды орындаудан соң нәтиже алынуы керек.
5) Машина универсалды , жан – жақты болуы керек, оның көмегімен кез – келген алгоритмді орындайтын болуы керек.
Сипатталған машинаның құрылғылары немесе структурасы қарапайым болса және орындалатын қадамдар элементарлы болса, алгоритмнің орындалуы машинаның жұмыс істеуі деп есептеуге болады .
Машинаның орындайтын қадамдары элементарлы болуы үшін белгілі бір алфавит арқылы ақпаратты алмастыру керек. Сондықтан алгоритм – кез– келген ақырлы алфавиттен берілгендерді немесе ақпаратты алмастыру
Ережелерінің ақырлы кез келген жүйесі.
Алгоритмнің анықталу облысынан алынған бастапқы берілгендер А аофавиті және ақырлы { 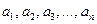 }таңбалар тізбегін құрасын, мұндай тізбекті сөз дейді. Алгоритмді орындау барысында жаңа сөз құрылады {
}таңбалар тізбегін құрасын, мұндай тізбекті сөз дейді. Алгоритмді орындау барысында жаңа сөз құрылады {  }, олар В алфавитін құрайды. Бұл алмастыруды жүргізу үшін келесі қадамдар орындалады:
}, олар В алфавитін құрайды. Бұл алмастыруды жүргізу үшін келесі қадамдар орындалады:
1) Бастапқы  сөзінің бір сөзін В алфавитінен
сөзінің бір сөзін В алфавитінен  таңбасымен алмастыру.
таңбасымен алмастыру.
2) Бастапқы сөздің таңбасын өшіру.
3) В алфавитінен бір таңбаны бастапқы сөзге қосу.
Егер алфавитке «бос таңба» деп аталатын таңба қосылса, оны сөзге оң жағынан да сол жағынан да қоссақ та сөз өзгермейді, яғни 1) операция бос таңбаны алмастыру болады. Сонда 2) – 3) – операцияларды орындасақ та, бәрібір 1) – қадамда тағы сол алдыңғы қадам қалады. Сондықтан абстрактылы машина әр символды зерттейді, сосын шексіз лентаға – жадыға сақтайды, егер символ бос болмаса оны басқа таңбамен алмастырады да жаңа қалыпта тұрады.
Бұл машина туралы теорияны Алан Тьюринг (1936-1937), Эмиль Пост сияқты ғалымдар ұсынған. Осы принципке сәйкестелген есептеу машиналары 8-9 жылдан кейін пайда болған.
Пост алгоритмдік машинасы алгоритм ұғымын дәлелдеуші
Бұл машинаның Тьюрингтен айырмашылығы – ол өзінің теориясында «машина» емес «алгоритмдік жүйе» деген терминді қолданған.
Оның абстрактылы машинасы бірнеше бірдей секцияларға бөлінген, оқу-жазу инесі бар шексіз лентадан тұрады. Әр секция бос немесе толтырылған болуы мүмкін. Лентаға түк жазылмаса секция бос, лентаға жазылып белгі түссе секция толық деп есептеледі.
Лента жағдайы процесс уақытында өзгермелі болды. Осы лента жағдайы мен оқу-жазу инесінің орны туралы ақпарат Пост машинасының жағдайын айқындайды.
Инені «  », метка-белгі М болсын. Секция бос болса, ешбір белгі түспейді. Бір қадам жасағанда ине оңға немесе солға 1 қадам жылжып белгіні салады немесе өшіреді. Программадағы командаларға сәйкес машина 1 жағдайдан келесі жағдайға көшіп отырады.
», метка-белгі М болсын. Секция бос болса, ешбір белгі түспейді. Бір қадам жасағанда ине оңға немесе солға 1 қадам жылжып белгіні салады немесе өшіреді. Программадағы командаларға сәйкес машина 1 жағдайдан келесі жағдайға көшіп отырады.
Әрбір команданың структурасы ХКУ болсын,
Х – орындалатын команда нөмірі,
К – орындалатын әрекет туралы нұсқау,
У – келесі команда нөмірі.
| № | команда | Командалардың жазылуы | Машина әрекетінің сипаттамасы |
| Оңға қадам | Х®У | Инені оңға қарай 1 секцияға жылжыту | |
| Солға қадам | ХУ | Инені солға қарай 1 секцияға жылжыту | |
| Белгі салу | Х V У | Секцияға белгі қойылады | |
| Белгіні өшіру | Х x У | Секциядан белгі өшіріледі | |
| 5 | Басқаруды ауыстыру |   Х У1
У2 Х У1
У2
| Секцияда белгі жоқ болса басқару у1 командасына, әйтпесе у2 командасына беріледі |
| тоқтату | Х стоп ! | Машина жұмысын тоқтатады | |
| Тармақты ұйымдастыру | ? a; b | Ұяшықты қарау, егер ұяшықта 0 тұрса, онда а номерлі командаға көші, әйтпесе b нөмірлі командаға көшу. |
Бұл әрекеттерге қойылатын қосымша шарттар:
- ХМУ командасы бос секцияда орындалмайды
- ХсУ командасы толық секцияда орындалады
- У командасының нөмірі программадағы бар команда нөмірімен сәйкес болуы керек.
Егер келтірілген шарттар сақталмаса, онда машина нәтижесіз жұмысын аяқтайды. Х стоп командасы нәтижелі орындалады. Себебі, ол өзінің алдындағы әрекеттер орындалып барып солардың нәтижесінде орындалады. Кейде машина тоқтамауы мүмкін, егер командалардың ешқайсысында тоқтау командасына көшу нөмірі болмаса.
Пост машинасы оң бүтін сандарды жазуды қарастырады, себебі кез келген сөз цифр түрінде кодталады.
Лентада К бүтін саны К+1 келесі белгіленген секцияларда, унарлы санау жүйесі қолданылып жазылады.
0,2,3 сандарыныің жазылуы:
| М | М | М | М | М | М | М | М |
Өзін тексеру сұрақтары
1. Алгоритмдік машиналардың шығуына не себеп болды?
2. Пост және Тьринг машиналарының айырмашылықтары?
Ұсынылатын әдебиеттер
1. Е. Бидайбеков, Е. Медеуов, А. Ниязбаев. Информатика бастамалары (алгоритмдеу). Алматы, 1990ж.
2. Вирт Н. Алгоритмы + структуры данных. Программы. – СПб, 2001ж.
3. Симонович С., Евсеев Г.Практическая информатика: Инфорком- Пресс, 1998г.
4. Острейковский В.А. Информатика, Москва, 2000 г.
5. Петров А.В., Алексеев В.Е., Ваулин А.С., Петрова М.А., Титов М.А., Шкатов П.Н. Вычислительная техника и программирование, Москва, 1990.
3-тақырып: «Алгоритмдік шығарылмайтын есептер. Есептелетін функциялар»
Дәріс жоспары:
- есептелетін функция ұғымы
- Рекурсия ұғымы, рекурсивті функция
- Компьютер көмегімен есептелетін функциялар теориясы.
- Черч тезисі
21-ші ғасырдың ортасына дейін алгоритм ұғымы есептеу әдістері ұғымымен теңестірілді. Есептеу әдістерінде қолданылатын арифметикалық, анализдік, тригонометриялық операциялардың орындалу алгоритм іспеттес болып жүрді. Ондай проблемаларды шешу үшін қосымша арнаулы дәлелдеулердің қажеті болмады. Ал 21-ші ғасырдың 2-ші жартысынан бастап сандық емес объектілерге қолданылатын алгоритмдерге қатаң формулировка берудің болмайтындығы белгілі болды. Лейбництің тұжырымдамасы бойынша алгоритмдік шешілмейтін есептер бар, сондықтан кез келген математикалық тұжырымдамалардың дұрыстығын дәлелдейтін алгоритм құрастыру қажеттігі туындады. Ол барлық теоремалардың дұрыстығын дәлелдейтін болуы керек.
Анықтама. Әлдебір алгоритм көмегімен есептелетін функцияны есептелетін функция дейді.
Іс жүзінде алгоритм – функцияны беру әдісі. Ал функция таблица, схема, формула түрінде берілуі мүмкін. Бірақ кейбір процестерде бастапқы енгізілген немесе берілген деректер мен алынған нәтижедегі деректер арасындағы байланысты ұйымдастыратын функцияны құру қиын, күрделі.
1 – бағыт Рекурсивті функциялар – есептелетін функциялар ұғымымен байланысты.
X және Y жиындары бар болсын. X жиынының кейбір элементтеріне Y жиынының элементтері сәйкес келсе, онда Y – те X – тен бөлшекті функция берілген дейді.
Y жиынында сәйкес элементтері бар және X элементтерден құралған жиынның элементтер жиыны функцияның анықталу облысы деп аталады.
X жиынында сәйкес элеметтері бар Y жиынының элементтер жиыны функцияның мәндер облысы деп аталады.
Егер X –тен Y-тегі функцияның анықталу облысы X жиынымен беттессе, онда ол функцияны барынша анықталған деп атайды.
Осы ұғымға және рекурсивті функцияға негізделіп алгоритмнің дәл анықтамасын құруға болады.
Кез – келген берілген деректерді (үзілісті, дискретті) әлдебір санау жүйесінде натурал сандармен кодтауға болады, онда
Олардың барлық алмастыруы есептеу операцияларының тізбегіне келтіріледі, ал өңдеу нәтижесі солайынша бүтін сан болып қалады. Кез келген алгоритм берілген сандық функция үшін бірдей, оның мәнін есептейді, ал оның элементарлы қадамдары қарапайым арифметикалық және логикалық операциялар болады. Мұндай функциялар есептелетін функциялар деп аталады.
Y(x 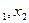 ,,,, x
,,,, x 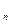 ) функция класы бар болсын. Аргументтер бүтін, нәтижеде бүтін сан немесе аргументі де нәтижесі де дискретті болсын.
) функция класы бар болсын. Аргументтер бүтін, нәтижеде бүтін сан немесе аргументі де нәтижесі де дискретті болсын.
Y(x 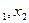 ,,,, x
,,,, x 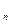 ) функциясы тимді есептелетін функция деп аталады, егер белгілі аргументтер мәндері бойынша оның мәнін есептейтін алгоритм бар болса.
) функциясы тимді есептелетін функция деп аталады, егер белгілі аргументтер мәндері бойынша оның мәнін есептейтін алгоритм бар болса.
Әр түрлі түсінілетін процесстер үшін есептелетін функциялар тізімі (алгоритмнің барлық қасиеттерін қанағаттандыратын) кәдімгі математикалық терминмен жеңіл сипатталатын функциялар болса, рекурсивті деп аталады.
Кез келген алгоритмдік модель, рекурсивті функция алгоритмнің элементарлы қадамын анықтауы керек, деректерді өңдеуге қажетті алмастыру тізбектерін қанағаттандыруы керек. Рекурсивті модельде мұндай элементарлы қадамдар қарапайым сандық функциялар деп аталады. S 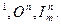
Бұл сандар комбинациясынан күрделі функциялар құрылады:
1) S  (x)=x+1 (бір аргументті бір орынды функция)
(x)=x+1 (бір аргументті бір орынды функция)
2) O  (x
(x 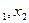 ,,,, x
,,,, x 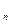 ) =0 –n орынды нөлге теңбе теңдік функциясы.
) =0 –n орынды нөлге теңбе теңдік функциясы.
3) I  (x
(x 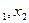 ,,,, x
,,,, x 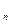 )=X
)=X 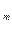 (1
(1 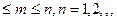 ) n орынды өз аргументтерінен 1 мәні теңбе теңді қайталану функциясы.
) n орынды өз аргументтерінен 1 мәні теңбе теңді қайталану функциясы.
Бұл функциялар барынша анықталған және интуитивті есептелетін функциялар. Бұл функцияларға қолданылатын қасиеттері бірдей барлық операциялар / операторлар қолданылады. Функцияларға осындай операторларды қолдану арқылы алынған бөлшек функцияларда бөлшекті рекурсивті функциялар деп аталады. Бөлшекті рекурсивті функциялар класы арифметикалық есептеулерді жүргізуге болатын функция кластарымен беттеседі.
Бөлшекті функцияның суперпозициясы
m – орынды f  функциялар n – орынды g (x
функциялар n – орынды g (x 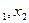 ,,,, x
,,,, x 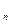 )
)
фу нкциясына қойылатын болсын. Нәтижеснде n – орынды 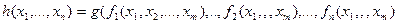 функциясы алынады.
функциясы алынады.
Мұны h функциясы g функциясынан 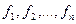 суперпозиция арқылы алынды деп айтады.
суперпозиция арқылы алынды деп айтады.
Мұндай қою -  деп берілгенді n- функция саны, олар келесі бір функцияның g-дің аргументтері ретінде қойылып тұр.
деп берілгенді n- функция саны, олар келесі бір функцияның g-дің аргументтері ретінде қойылып тұр.
Егер 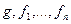 функциялары есептелетін болса, n- функциясы да есептеледі. Онда
функциялары есептелетін болса, n- функциясы да есептеледі. Онда 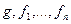 функциялары интуитивті есептелетін болса, n- функциясы да интуитивті есептеледі.
функциялары интуитивті есептелетін болса, n- функциясы да интуитивті есептеледі.
Мысалы:
1)  -ді табу керек.
-ді табу керек.
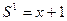 ,
, 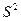 -ні табу үшін
-ні табу үшін 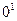 -ді
-ді  -ге қою керек, ал
-ге қою керек, ал 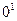 =0 сонда
=0 сонда 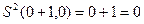 .
.
2) 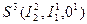 -ді табу керек.
-ді табу керек.
N=3-1=2 – нәтиже 2-орынды функция болады:
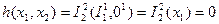 .
.