Скорость и ускорение в декартовой системе координат
В декартовой системе вектор положения задается в виде
 ,
,
где  координаты вектора, а
координаты вектора, а  ,
,  – ортонормированный базис, т. е. базисные векторы единичные и взаимно - перпендикулярные (рис. 3.1,а). В этом случае координаты равны проекциям вектора на оси, задаваемые базисными векторами:
– ортонормированный базис, т. е. базисные векторы единичные и взаимно - перпендикулярные (рис. 3.1,а). В этом случае координаты равны проекциям вектора на оси, задаваемые базисными векторами:  .
.
Векторы скорости и ускорения:
 ,
,
а их модули 
3.2. Скорость и ускорение в цилиндрической системе координат
Вектор положения задается как функция цилиндрических координат  :
:
 (3.2)
(3.2)
В цилиндрической системекоординат (рис. 3.1,б), каки в любой другой системе, базисныевекторы вводятся как частные производные по координатам от  :
:
 (3.3)
(3.3)
Базисные векторы направлены по касательным к координатным линиям – линиям, получающимся при изменении только одной координаты.
| Рис. 3.1.Описание движения точки
|
Использование единичных базисных векторов  удобно тем, что координаты вектора в единичном базисе имеют ту же размерность, что и сам вектор.
удобно тем, что координаты вектора в единичном базисе имеют ту же размерность, что и сам вектор.
Дифференцируя (3.2), получим с учетом (3.3):
 . (3.4)
. (3.4)
Дифференцируя (3.4) и учитывая, что  , получим:
, получим:
 . (3.5)
. (3.5)
 ,
, координаты вектора, а
координаты вектора, а  ,
,  – ортонормированный базис, т. е. базисные векторы единичные и взаимно - перпендикулярные (рис. 3.1,а). В этом случае координаты равны проекциям вектора на оси, задаваемые базисными векторами:
– ортонормированный базис, т. е. базисные векторы единичные и взаимно - перпендикулярные (рис. 3.1,а). В этом случае координаты равны проекциям вектора на оси, задаваемые базисными векторами:  .
. ,
,
 :
: (3.2)
(3.2) :
: (3.3)
(3.3)

















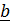


 удобно тем, что координаты вектора в единичном базисе имеют ту же размерность, что и сам вектор.
удобно тем, что координаты вектора в единичном базисе имеют ту же размерность, что и сам вектор. . (3.4)
. (3.4) , получим:
, получим: . (3.5)
. (3.5)