Сурет 9.1.

Сурет.

Дәл қазiр сандық әдiстер әлемдерде (ШЭӘ ) шектi элементтер әдiстерi болып таралған. Оларға жатады:

1.күрделi геометрияның облыстары үшiн бiр қалыпты торлар, екi өлшемдi және үш өлшемдi жағдайлардың есептеу мүмкiндiгi;

2."технологиялықтық" әдiстер (түзету бұдан әрi)

Қазiргi ШЭӘ XX ғасырдың 50-шi жылдарында серпiмдiлiк теориясының есептер шешiмiнде пайда болды.

Өзi таралған статикалық есептер - жүктелген конструкция туралы есеп

 

Ω облысы — күрделi. Мысалы, облыс 7.1- сурет көрсетiлген түрдi иемдене алады. Әрбiр оңай төменгi облыс - шектi элемент.

ШЭӘ ге дәл қазiр (Ритц ) вариациялық және (Галеркин немесе Бубнова - Галеркин) проекциялық әдiстердiң бүтін бөлігін түсiнедi.

Ритцтың вариациялық жолы

Екi есептi қарап шығамыз:

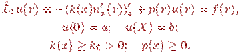(7.1)

(7.2)

Бұл есептер ұқсас: (7.1 ) бiр өлшемдi жағдай (7.2 ) ортақ есеп болып табылады. (7.1 ) теңдеулер (7.2 ) және өздiгiнен түйiндендiру формасында жазып алынған. Функционалдар сәйкестiгіне байланысты (7.1 )және(7.2 ) есептеріне шарт қоямыз

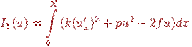(7.3)

және

(7.4)

Нормамен (Соболев кеңiстiгі) функциялар кеңiстiгiн қараймыз

Бұл - шектелген интегралы бар функция.

Теорема 5.Жеткiлiктi шектi шарттардың барлық функцияларының арасында, (7.1 ) есептiң шешiмi (7.3 ) функционалға ең кiшi мән беріледі, ал шешiм (7.2 ) - (7.4 ) функционал ретінде.

Ритц әдiсiнiң ортақ схемасы

Есептiң шешiмiн (7.1 ) түрінде iздейдi

(7.6)

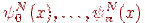-базистық функциялар шекаралық жағдайды қанағаттандырады, ал 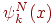үшін 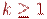, Егер (7.6 ) жинақтауда шексiздiкке дейiн болса, онда бұл формула (7.1 ) есептiң дәл шешiмiн бередi. Базистiк функциялардың шектi саны қаралады, онда тек қана жуық шешiмін аламыз. Мысалы, Ритцтың әдiсi үшiн базистiк функциялардың тригонометриялық негiз қызмет көрсете алады, жуық шешiм ретінде Фурье қатарының шектi кесiндiсiн аламыз.

(7.6 )- ны (7.3 )-ке қоямыз, сонда

(7.7)

(7.7)шартынан функционалдық минимумын табамыз

C_k коэффициенттерiнiң анықтауы үшiн N сызықты теңдеуінен жүйесiн аламыз. Содан есептiң шешiмiн (7.6) деп жариялаймыз.

Дәл осылай (7.4 ) функционал үшiн түсемiз. Коэффициенттердi анықтау үшiн теңдеулер жүйесiндегi сан ол да N (у бір ғана индекстi базистiк функцияда!) болады. Ұқсас функционалдың түрi (7.7 ) болады, бiрақ кесiндi бойынша интегралдар орынына кеңiстiктiң қаралатын облысы Ω бойынша екi есе шығын интегралдар, ал туындылардың орынына – градиенттер тұрады.

Ритц әдiсiнде пайда болатын бiрiншi мәселе – базистің қолайлы таңдауы. Функциялардың жиыннан шешiмге тәуелдi бола ма? Қате қалай бағалайды?

Базистiң екi түрі болады: Ритц әдiсi үшiн финит сақтаушысы бар функциялар базисі жәнеглобалдi базис.

Ритц әдiсiн қажетті және жеткiлiктi шешу үшiн және сызықты комбинация бар болу үшiн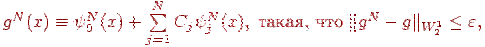

егер есептеулер тура жүргiзiлсе.

Ритц әдiсiндегi қолдану үшiн мүмкiн базис

q = 1, ..., N.

 

Базис [0, 1] кесiндiде: T_j(x) — j - Чебышевтiң полиномы;

Ритц әдiсiнiң базисі бойынша жiктеуiнiң коэффициенттерiн анықтау үшiн сызықты теңдеулер жүйесiнiң толтырылған матрицасы пайда болады. "Сәтсiз" қолданулар базис жағдайында оның саны жеткiлiктi.

Ритц әдiсiнiң технологиялығы төмендегiдей болады. Тиiстi жүйенiң матрицасы өздiгiнен түйiндес диагонал көбі базистің дұрыс таңдауында болып табылады. Итерациялық әдiстермен қиындатылған жүйенi жылдам шешуге болады.

Сурет.

Финит сақтаушысы бар функциялар базисін қолдана отырып, Ритц әдiсiн қарапайым вариантын қарап шығамыз. x нүктелерiнiң жиыны үшiн функцияның сақтаушы екенін ескертемiз. x_j (торды ) нүктелерiнiң [0, X] кесiндiсiне бөлiктеу енгiземiз: 0 = x₀ < x₁ < ... < x_n = Х. Базистiк функцияларды саламыз:

екенін базистің кемшiлiгi интегралдар және туындылар қорытылған функциялармен анықталатынын тексеруге болады. Бұл базис қадыры базистiк функциялар ортогоналы болып табылады.

болсын, онда

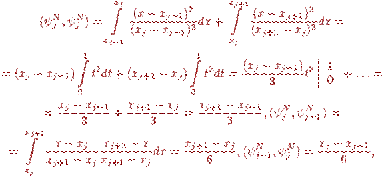
ал қалған барлық скалярлық көбейтулер нөлге тең.

Сонымен бiрге, базистiк функциялардың туындылары интегралдарға оңай алу жеткiлiктi. Әрбiр мұндай базистiк функцияның сақтаушысы шекті элемент деп аталады, мұндай базистің қолдануы бар Ритц әдiсi - ШЭӘнiң бiрiншi әдiсi. Сонымен бiрге кейде шектi элементін финит сақтаушысы бар базистiк функциялары деп атайды.

Галеркиннiң проекциялық әдiсiнiң тұжырымы

(7.1 ) және (7.2 ) есептi бұрынғыша қараймыз.

Дифференциалды операторларды сынып ендiгәрi қарастырылады. Ритц әдiсiнiң басты жетiспеушiлiгi - тек қана вариациялық тұжырым рұқсат ететiн дифференциалды есептерге қолданылады, яғни сызықты жағдайда - өздiгiнен түйiндендiрілген оң нақтылы (барлық меншiктi сандар оң ) оператор.

Қатар (7.1 ) және (7.2 ) тұжырыммен жазуды пайдалана (қорытылған ) әлсiз шешiм анықтаймыз: (7,8)

v -кез келген функциясы бұрын функционалдық кеңiстiктен қарастырылған, скалярлық көбейту сияқты анықталған

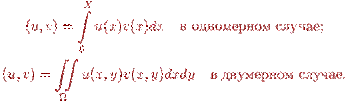
(7.8 ) теңдiгі есептiң қорытылған шешiмiн анықтайды. Егер белгiлi u- есептiң классикалық шешiмi, онда ол (7.8 ) қорытылған шешiмнің мағынасы болып табылатыны белгілі. Керiсi, түсiнiктi себептер бойынша, қате - C¹ немесе C² қарағанда функциялар "көбiрек". Есептерде қорытылған шешiм бар бола алады, бiрақ классикалық болмауы мүмкін.

Енгiзiлген базисі бар кеңiстiктiң шектi өлшемін iшкi кеңiстiгiне қарап шығамыз:

- базистiк функциялар Ритц әдiсi үшiн 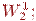олар базистiк функциялар қасиеттермен болуы керек. 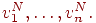бұдан (7.8 ) орынына енді таразы функцияларының шектi жүйесi (7.8) үшiн қарап шығамыз. (7.8) орнына таразының функцияларына шектi жүйесiне проекциялауын қарап шығамыз. Сонымен түсіндірмесін енгiземiз

(7.9)

бұл жерде R - байланыссыздық. (7.8 ) базистiк функциялар бойынша жiктеудiң алмастыруларынан кейiн, байланыстардың жүйесiн аламыз

(7.10)

Функциялармен байланыссыздыққа 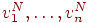осындайда жетедi, оның ортогональ қосымшасына жатуға анықталатын кеңiстiктегi байланыссыздықтың минимумы: барлық k үшiн . Ендi таразының функциялары базисті құрастырту үшiн талап етуi керек. Табиғи базистiк таразының функциялар ретiнде қолдану. Осыдан Галеркин проекциялық әдiсiн аламыз.

немесе матрица турінде:

 

Бұл байланыстар коэффициенттердiң Ритц әдiсi үшiн теңдеулер жүйесiнiң қорытындысында пайда болады.

Сызықты дифференциалды оператордың түйiндесін скалярлық көбейтулердi есептеуге қолданылды. (7.10 ) оператордың байланыс түйiндестiгi қорытындыда қолданылмады. Демек , Галеркин әдiсi дифференциалды оператор (сызықты емес) жағдайға және жалпылауға болады. "Функциялар - қақпақтары" жоғары енгiзiлген қолдануларда базистiк функциялар ретiнде ШЭӘ тәсілін аламыз. (7.1 ) және (7.2 ) есептер әдiсі үшiн Ритц әдiсi байланыста болады.

Шектi элементтердiң сұлбасын құрастыруға мысал

Есептер санының кiшiрейтулерi үшiн санаймыз

(7.1 ) есептiң өздігінен кездеспейтін аналогiн қарап шығамыз:

Кездесетiн теңдеудi табамыз:

Бұл байланыстан 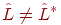шартын оңай аламыз. Базис бойынша жiктеудi ендi жазып аламыз:

бастапқы дифференциалды теңдеуге қоямыз:

Сол бөлiктегi әрбiр қосындысын бөлек қарап шығамыз:

( 7.11)

Алғашқы екi қосылатын оң бөлiктерде базистiк функциялардың сақтаушылары финит болғанда пайда болады. Соңғы қосындысы оң бөлiгiнде интегралдаумен пайда болады. Не үшiн бөліктеп интегралдау керек? Демек, бұл - базистiк функцияның туындылары, бiрақ сырттай қарағанда - скалярлық көбейтулердегi қорытылған функциялар, ал - функция, күрделiлiктер интегралдауда пайда болады.

Қорытындылай келгенде , C_k кейін алдында коэффициентін есептеу қажет.

k(x) функциясы үзiктi болып есептеледi. Кесiндi ретiнде есепке ала отырып қалған функцияны қандайда болмасын 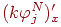аппроксимацияны қолдану тиiс.

Алғашқы екi қосылатын (7.11 ) оң бөлiктерде шектi шарттардан C_k тәуелдi болады және анықтау үшiн теңдеулердiң оң жүйенiң бiр бөлiктерi жатады.

Ендi қарап шығамыз

C_k коэффициенттері келесi болады:

Бұл жерде q(x) функциясы тұрақты және үзiктi деп есептелінеді.

p (x ) соңғы қосынды өрнегін бередi

яғни есептелетiн интегралдардың әдiсiн ұқсас Нумеровтың аппроксимациясы ретінде iс жүзiнде аламыз. Сонымен бiрге, мағыналы айырмашылық бар болады. Торлы функция - бұл берілген кестелiк функция. ШЭӘ (жуық ) шешiм - бұл торлы функция емес, жай ғана элемент

Базистiк функцияларды құрастыру

ШЭӘ математикалық базис - Галеркин әдiсi және Ритц вариациялық әдiсi - екiншi XX ғасырдың он жылдығынан бастай дамыды. Соңғы жылдардың ШЭӘ-сiне өрлеу деп аталатын үйлесiмдi базистік жеткiлiктi тегiстiкке ие болатын базистiк функцияларының жиындарының құрастыруында болады.

Базис "қақпақтар"- дан екi өлшемдi жағдайда . Базистiк функциялардың процесстің құрастырулуы:

• облыстар триангуляцияны – әрбiр базистiк функциясының сақтаушысы болып табылған үшбұрыштарға бөлiктеу;

• базистiк функцияларды құрастыру.

(7.3- сурет белгілену) триангуляциялық талаптары.

7.3- сурет.

Мысалдар үйлесiмдi базистiк функцияларға. Егер "Қақпақтар" базисі қолданылса, онда ШЭӘ шешiм (шектi элементтердiң ұштастыруының жанында) әрбiр түйiнде бiрiншi туындының үзiлуiн алады. Бұл ШЭӘ-нiң базис таңдауы артынан болады. Ізделiп отырған функция үздiксiз.

Үздiксiз бiрiншi туындыға ие болатын шешiм табу керек. Базис функцияларының жиынын саламыз:

Шекті элементтің өлшемі 1 ге тең деп аламыз. Бiр өлшемдi тор әрбiр элемент үшiн сызықты өрнектеу табылады, 1-шi ұзындықтың кесiндiсiне аударатын осы элемент. Базис функциясы бар болатынын қоямыз

Әрбір кесіндіде [- 1;0] , [0;1]-полиномы. x = ± 1 нүктеде және оның туындыларында m – 1 ретімен нөлге тең. x = 0 нүктеде

Онда j = 0, ..., N; i = 1, ..., m – базис болады.

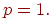жағдайын қарастырамыз. онда әрбір кесіндіге функция сызықты болады.

p = 3 аламыз, онда m = 2. Базис функциясын құрамыз.

i = 1 қарастырамыз. [- 1;0], [0;1]кесіндіден 3 полином дәрежесін аламыз.

Шарт: , , , коэффициенттерін анықтайды

a₀ = 1; a₁ = 0; a₂ = - 3; a₃ = - 2

Барлық кесіндіде [- 1;0]

Ұқсас [ 0;1] кесіндісінен бұдан аламыз.

Базистік функция графигі 7.9 сурет. көрсетілген

7.9 сурет

i = m = 2 болсын.

мына шарттан , шығады. Ұқсас Функцияның графигі 7.10 суретінде көрсетілуде

7.10 сурет

Егер p + 1 жоғары емес барлық базистiк функциялар дәреженiң теңдеуi үшiн (C^m жатады) үздiксiз болса базис үйлесiмдi болып табылады.

Галеркин әдiсi мұндай базисті қолданана ма? Енді торлар нүктесінде (элемент аралық ) u функциясын білу емес, бірақ ол x: бойынша туындысын бiрiншi, екiншi, ...., (m - 1)бiлу керек.

u(a + jh) и u'_x(a + jh) Галеркин әдiсiнiң теңдеулер шешiмiнде сандық анықталатынын атап өтемiз.

Базистiк функциялар және жiктеудiң коэффициенттерiнiң саны үлкейдi.

Сонымен бiрге сирелген жүйенің матрицасын байқаймыз, бiрақ (екiншi жүйенiң ретi жоғары болса ) үш диагоналды емес.

7.11 сурет

Екi өлшемдi жағдайдағы келiсім. (7.11-сурет) келесi қапсыру шамалар керек: түйiндегi 18 шамалары плюс нормалы туындылардың мәндерi шегiнде.

Демек кез келген тұрақтыны 21 алу керек, бұдан 21 шарт пайда болады. Полином алу керек (көпмүшелігі x⁵, y⁵дейін) жоғары дәрежесі жеткiлiктi болса. Сондықтан келiсiлмеген базистiк функциялар немесе (m = 1 ) төменгі тәртiбiмен қолданылатын көп өлшемдi жағдайда келiсу.

Өзiн-өзi тексеру тапсырмалары:

1 )Шектi элементтер әдiсiнiң базис түпкі идеясы қандай?

2 )Ритц вариациялық жолы туралы әңгiмелеңiз.

3 )Базистiк функциялардың құрастыруы туралы әңгiмелеңiз.

13 дәрiс. Ыдырау әдiстерi.

Дәрiстiң мақсаты: ыдырау әдiстерiне әртүрлi тектi ортақ ұсыныстар беру.

Тақырып сұрақтары:

1 )Ыдырау әдiстерi туралы ұғым.

2 ) Бiрiншi және екiншi τ дәлдiк ретi бойынша ыдырау әдiсі.

3 ) Компонент бойынша ыдыраудың кезеңдiк әдiстерi.

4 )Оператордың факторизациясымен ыдырау әдiстерi.

Қысқаша тақырып мазмұны:

Ыдырау әдiстерi туралы ұғым

Тұрақты коэффициенттерi бар туындылардың бөлiндiлерiндегі теңдеу үшiн дифференциалды есептi қарап шығамыз:

(8.1)

бұл оператор – тұрақты коэффициенттерi бар оң дифференциалды оператор. операторы бойынша туындыларға кеңiстiктiң айнымалы кiредi. кез келген нөл емес элемент үшiн орындалған. Γ — интегралдау облысының Ω_x шекарасы. Λ — айырма оператор аппроксимациялайтын. Айырма теңдеуін тексеруге болады

(8.2)

Екiншi ретпен τ дейiн (8.1 ) аппроксимация жасайды (Кранк-Никольсон сұлбасы).

[tⁿ, t ^{+ 1/2}], [t^{n + 1/2}, t^{n + 1}] жазып алған аппроксимациялардың бiрiншi дәрежесiнiң анық және анықталмаған сұлбаларын кезектескен қолдануды нәтиже сияқты түсiндiруге болатынын байқаймыз

(8.3)

Аралық жiктегi (8.3 ) теңдеулер функциясының мәндерiн алмағанда (жартылай бүтiн индекспен) әр уақытта, (8.2 ) аламыз. Егер , онда

(8.4)

Сонымен бiрге айырма операторы оң болып табылады

Келесi жiктегi шешiм операторлық түрде төмендегідей әр уақытта жазып ала алады

немесе

онда

Алған айырма теңдеудiң орнықтылығының дәлелдерi үшiн (8.4) скалярлық көбейтемiз, (uⁿ + u^{n + 1})/2 аламыз

(8.5)

Дұрыстыққа байланысты айырма операторы , онда (8.5) сұлбасының орнықтылығы қамтамасыз еткенi шығады. Егер айырма Λ оператор болса жоғарғы және төменгi қабаттар айырма операторлардың жартылай сомасы түрiндегi таңдалған (кеңiстiк айырымдары) әр уақытта болады.

Онда схема бойынша τ аппроксимацияның екiншi ретiне ие болады.

Бiрiншi және екiншi τ дәлдiк ретi бойынша ыдырау әдiсі

Жергiлiктi – бiр өлшемдi сұлбалар

Айырма оператор оған сәйкес дифференциалды оператор қоямыз әрбiр сәйкесiнше бiрсарынды тек қана кеңiстiктiң айнымалы және айырымның тек қана бiр-бiрдендегi туындылары бойлай қосатын операторлардың сомасының түрiнде көрсетуге болады. Жинағы кеңiстiктiң бағыттары N. Мұндай дифференциалды және айырма операторларды жергiлiктi– бiр өлшемдi деп атаймыз. Дифференциалды және айырма операторлар сомасы жергiлiктi – бiр өлшемдi түрiнде жазылады:

Бiркелкi есеп үшiн бағыттар бойынша ыдыраудағы сұлбаны көшiрiп алуға болады:

Әрбiрi бастапқы дифференциалды аппроксимация жасамайтын айырма теңдеулердiң жүйесi алынған, бiрақ оңай (егер айырма операторлар тек қана алғашқы және екiншi айырымдарда болса бойлай тиiстi бағыттың прогонкасының әдiсiмен) шешiле алады. Әйтсе де, басқа, оларда дәйектi түрде қолданылған бірінен соң бірі дәлдiгi бар шешiм келесi жiкте әр уақытта бередi. Қабатты өткелiнiң қорытынды операторы жиынтық аппроксимация орын алатынын айтады. Әдiс жоғарыда айтылған кейде бөлшектi адымдардың әдiсiмен деп атайды, жылу еткiзудi көп өлшемдi теңдеудiң шешiмiнде және одан тарлау кездестi.

Ыдырауды сұлбаның варианттарының бiртектi емес есебi үшiн болуы мүмкiн

Мысалы, кiрiспе оны барлық теңдеуiндегi оң бөлiктiң есепке алуының тағы басқа әдiстерi (келесi жiктегi аппроксимацияның қатесiнiң минимизациялауы әр уақытта) ең жақсы жиынтық аппроксимацияның шарттарынан жиналып алынатын таразының көбейткiштерiмен болуы мүмкiн.

Бағыттар бойынша ыдыраудың жоғары келтiрiлген сұлбалары абсолюттi орынды.

Ыдырау әдiстерiнiң ортақ тұжырымы

Жергiлiктi алмастырамыз – бiр өлшемдi дифференциалды операторлар айырма операторлармен келесі көрiнiстегi ыдырауды сұлбаны ортақ түрде көремiз:

Мұндай ыдырау сұлбаның орнықтылығының шарты болады. Ыдырау сұлбасы өлшем коэффициенттері мына түрде көрсетілген

Егер ыдырауларды бұл сұлбаға жоғарғы және төменгi қабаттардың салмағы Λ_i қойса онда γ = 0, 5, жалғастыратын операторлардың жағдайында (әрбiр мұндай айырма оператор екiншi тиiстi шамасында жергiлiктi аппроксимация жасайды - бiр өлшемдi дифференциалды оператор) сұлба аппроксимацияның екiншi ретiн әр уақытта алады.

Егер бұл әрбiр оператор болса, онда сұлба абсолюттi орнықты болады.

Жылу еткiзудi теңдеу үшiн ыдырау сұлбалары

Жылу еткiзудi тұрақты теңдеудi қараймыз

Мұнда Лапласа операторы анықталған Сонымен бiрге оны үш сома жергiлiктi - бiр өлшемдi операторлар түрiнде жазып алуға болады . Сәйкесінше оператор айырмасы болады егер екiншi айырма туындының есептеуi ұқсас операторларымен анықталады және қалған бағыттар бойынша Λ_yy, Λ_zz жергiлiктi - жылу еткiзудi сұлбасы теңдеу үшiн бiр өлшемдi болады

Аппроксимация ретiнiң жоғарылату үшiн салмақтар сұлбасын пайдалануға болады

Компонент бойынша ыдыраудың кезеңдiк әдiстерi

Әдiстер ол үшiн Λ_i операторлардың коммутативтiлiгi талапты болмайды.

(8.1 ) сандық шешiмін қарастырамыз, [tⁿ, t^{n + 1}] кесiндiде, [t^{n - 1}, t^{n + 1}]екi бiртiндеп адым. Ендi айырма жергiлiктi - бiр өлшемдi операторлар уақыттардан анық тәуелдi болады, олар сонда кесiндiнiң ортасында анықталады. Ыдырау сұлбасын жазайык:

(8.6)

Бұл әдiс операторлық формада жазылады, мағынасы

Математикалық физиканың кейбiр есептерi үшiн ыдырау кезеңдiк әдiсін қолданудың мысалдарын қарап шығамыз.

1- Мысал. Диффузияның үш өлшемдi тұрақты теңдеуi, интегралдауды облыс – параллелепипед болады. Тiк жазықтықтағы диффузиясының коэффициентi (0z өсі) тiк бағыт геофизиканың есептерi үшiн тән координатадан тәуелдi болады ма? — көлденең жазықтықтағы диффузиясының коэффициентi. Есеп түрiнде көрсете алады

үш бiр өлшемдi есептердiң бiртiндеп шешiмiне қаралатын үш өлшемдi есептiң шешiмiн түйiстiремiз. Бiрiншi есеп болады

ол тiк жазықтықтағы диффузиясын суреттейдi. Екiншi және үшiншi есептi жазып аламыз

Енді бастапқы дифференциалды теңдеудiң айырма аппроксимациясын қарап шығамыз

Циклдiк компонент бойынша ыдырау айырмасы сұлба түрін алады

 

Оператордың факторизациясымен ыдырау әдiстерi

Ыдырау сұлбасы факторизациялануы

Дифференциалды есептер шешiмдерi үшiн

айырма сұлбасын n = 0, 1, ... қолданамыз.

Fⁿ

Мысал. (бойлай-көлденең схемасы) айнымалы бағыттар әдiсi. Жылу еткiзудi сызықты екi өлшемдi теңдеудiң шешiмi үшiн сұлбаның жазылуын келтiремiз. Есептеу формулалары бар

Онда u^{n + ½} санап, операторлық түрін аламыз

немесе

Айырма сұлбасы факторизациялау сұлбасы түрінде берілуі мүмкін.

Анықталмаған сұлба ыдырауы жуық шамамен факторизацияланады.

Анықталмаған айырма сұлбасын қарап шығамыз

(8.7)

(8.7) айырма сұлбасы түрінде берілсін деп ойлайық

(8.8)

 

Өзін –өзі тексеруге арналған тапсырмалар:

1. Ыдырау әдісі туралы әңгімелеңіз

2. Бірінші және екінші ретті қандай ыдырау әдістері бар?

3. Факторизациялау операторымен ыдырау әдісі қалай байланысады?

 

 

14-15 дәріс. Айырма сұлбаларын құрастыру үшiн қолданылатын вариациялық қағи.

Дәрiстiң мақсаты: айырма сұлбалардың вариациялық қағидаларының қолдануы туралы ортақ ұсыныстар беру.

Тақырыпқа сұрақтар:

1 ) Гамильтонның қағидасы.

2 ) Қисық сызықты торда жылу еткiзудi теңдеу үшiн Вариациялық схема.

3 ) Өзіндік есептер.

Қысқаша тақырып мазмұны:

Ең кiшi әсер қағидасының (Гамильтон ) қолдану мысалы

1 ұзындығымен қатты созылмайтын сырықтың қозғалысы туралы есептi қаралады. Ол нүктеге 0 бекiткен, сырықтың басқа аяғына (9.1- сурет) күштейдi. Сырықтың қозғалысын анықтауға керек болады. Сырығының бастапқы формасы тап қалған болып есептеледi .

9.1-сурет

Мүмкін болатын шешiмдер : қозғалыстың теңдеуiн жазып алсын - гиперболалық түрдiң теңдеуi алады; шектi шарт қою; айырма сұлбаны құрастыру. Есепте бiрақ сырықтың керектi мөлшерде үлкен тербелiстерi рұқсат етiледi.

Шешiмнiң басқа әдiсi. Енгiземiз θ — s доғасының ұзындығы, t уақытының функция x тың өстерi ауытқудың бұрышы. Сонда аламыз

кинетикалық энергияның кағы бар

кинетикалық энергияның кағы бар ал потенциялдық энергия аз энергиядан жинақталады және ішкі күші : (1 коэффициентіне сәйкесінше тең болады)

L = T – U Лагранж жүйесі болады

Гамильтонның қағидасына сәйкес, әсердiң функционалы шын қозғалыстағы экстремалдық мәнге жетедi. Бұдан шығады және мынандай теңдеу аламыз

Интегро - анықтау үшiн дифференциалды теңдеу Ө(s, t), және де қалай оның айырма аппроксимациясын салу - түсiнiксiз. G(s, σ) атап өтемiз w''= - g(s), w'(0) = w(1) = 0 есебi үшiн Гриннiң функциясы бар.

9.2 сурет

Ендi L_h Лагранж дискреттi аналогiн енгiземiз. Ол үшiн бiрдей Δl ұзындықтың кесiндiлерiнiң стерженге бөлеміз( бiрдей масса). Әрбiр кесiндi θ_k көлбеу бұрышымен бейнеленедi (9.2 сурет)

Шектi элементтер немесе орталық айырымдары бар сұлбалардың аналогi пайда болды. Өрнек интегралдары шектi бұрылыстармен алмастырған, бұл интегралдар iс жүзiнде трапециялар әдiсiмен есептеген, яғни L_h лагранж анықтауындағы O(Δl)² қателiгі бар. Енді теңдеулер жүйесінің қатарын жазамыз.

яғни, енгiзiлген торда барлық мәндерге арналған функционалдың дискреттiк аналогi дифференциалданады. Соңғы теңдiк қаралатын есептер үшiн байланысқа алып келедi

бойынша лагранждың дискреттiк аналогiнiң соңғы өрнегiне және дифференциалдауды орындау алмастырулардан кейiн аламыз:

Осылайша гамильтонның вариациялық қағидасының торлы аналогiнiң қолданғанда , дифференциалды – айырма теңдеулер жүйесі алынды (уақыт бойынша дифференциалды, айырма кеңiстiк бойынша айнымалы).

9.3- сурет.

Бұл жүйені қарапайым дифференциалды теңдеу секілді шеш біраз қиын болады, өйткені ол Кошидің нормалы формасына келтірілмеген. Бірақ соңғы дифференциалды – алгебралық жүйемен жұмыс істеп шешуге болады. Шешімдердің алгоритмінің негізі glk - Гриннiң функциясының торлы аналогы болған. Кері матрица оператордың екінші туындысының торлы апроксимациясы. Толығырақ [19.1 ]

Қисық сызықты торда жылуөткізгіш теңдеу үшiн вариациялық сұлба

9.5-сурет.

Жылуөткізгіштік сызықты теңдеуді қарастырамыз:

(9.1)

Шекаралық шарттарымен

қисық сызықты Ω шектелген шекарамен. Сонымен қатар теңдеуінде де ешқай жерде азғындалмаған, яғни k(x, y) > 0 облыстың барлық нүктелерінде, шекаралық нүктелерін қосқанда. Ω шектелген облысында төртбұрышты ұяшықтары бар тор енгізілген. Тор қисынды болып есептеледi, яғни ұяшықтардың кез келген екi төбелерi үшiн бөлшектенген, оларды біріктіретін және ұяшық қабырғаларынан тұратын (9.5- сурет).

Ω облысын ішінде бірдей өлшемді торы бар параллелограмға (тiк төртбұрыш ) ауыстыратын, түрлендіруі бар тор құрылған болсын.Онда x, y координаталық сызығы ξ, η қисықсызықты базисі қисық координатаға көшеді.

(9.1 ) теңдеуін жүйе түрінде жазамыз.

(9.2)

Функционалды қарастырамыз

(9.3)

табамыз:

Бұдан функционалдың минимумы жылуөткізгіштік теңдеуінің шешiмiнде жетедi.

Айырымдық сұлба үшін , функционалының дискретті аналогын енгіземіз, яғни дискретті аналогта есептік мәні жылу ағыны болады.

Функционал құрастырудан бұрын, (9.6- сурет) айырма тордың ұяшығын қарап шығамыз. Uij және kijдiң (немесе жылу өткiзгiштiк) жылу еткiзуiн коэффициент температураны (диагональлердiң қиылысу нүктесiне) ұяшықтың ортасына жатқызамыз. Келесіде термодинамиялық шама барлық ұяшықта тұрақты деп санаймыз. Жылу ағынының векторлары (9.6- сурет) ұяшықтың бұрыштарына жатқызамыз, ал тиiстi қабырғалардың орталықтарына - координаталық өстерге ағындардың проекциясын жатқызамыз. I координатаның үлкеюiн ξ шара бойынша үлкейетiнiн санаймыз ; j η үлкею өлшемі бойынша ; ағынның векторларының проекциялары бойлай тиiстi координаталық сызықтарға бағытталған. Сыртқы нормалдың векторлары бар екi ұяшық үшiн

9.6 сурет

Теңдеуін интегралдайық

Айырымдық тордың элементарм ұяшығы бойынша мынаны аламыз:

(9.4)

Мұндағы Г- сәйкес қабырғаларының ұзындығы, S_ij - элементар ұяшықтың ауданы.

Дөңес төрт бұрыштың барлық төбелерiнің координаталары белгілі болғандықтан, ұзындықтарды, аудандарды және бұрыштардың iздестiруi - қарапайым геометриялық есеп болып табылады.

(9.4) теңдеу - (9.2 ) теңдеудiң дискреттi аналогi. tⁿ, t^{n + 1} уақыт моментінде барлық ағандарды анықтауға болса, содан кейін (9.2 ) аппроксимацияны әр уақытта қандай болмасын өлшеммен қолдануға болады, онда температура өлшеміне айырымдық сұлба құрылады.

Мынаны ескеремiз

(9.3) ке дискретті аналогін құрамыз

(9.5)

Функционалдың дискреттi аналогiнiң бiрiншi қосындысына кiретiн скалярлық квадраттар, контрвариантты проекция арқылы өрнектеледі (9.7-сурет) .

және т.с.с

9.7 сурет

"+" немесе "-" таңбалары ереже бойынша анықталады: "+" ағынның компонентi, егер сыртқы нормалы бар бағытталған ағынының проекция болса. Егер қарама – қарсы болса "-" . Сайып келгенде, және бұрыштардың ұяшықтары үшiн "+" таңбасы, ал және бұрыштары үшін "-" таңбасы болады (әртүрлi таңбалардың шығармасындағы жылу ағынының проекциясы) .

 

Анық сұлба алу үшiн, σ = 0 жоғарғы салмаққа қабатын(9.5 ) ке қойып және W_ξij, W_ηij бойынша дифференциалдаймыз. Туындыны нөлге теңестіріп алып, ағындардың анықтау сұлбасын аламыз, соңында (9.4) тен іздейміз.

(9.4) анықталмаған сұлбаны құрастыру үшiн σ = 1 деп санаймыз, ал (9.5) орнына дискретизацияны жазамыз:

Тәуелдi болатын өрнектi (9.5 ) мәніне болғанша анық көз жеткіземіз. бұдан белгiсiз қарсы проекциялардың квадраттар қосындысы бар. Дифференциалдай отыра, ағындарды анықтау үшiн теңдеулердiң сызықты жүйесiн аламыз. Жүйенiң матрицасын келесi қасиеттерге ие болатынын көрсетуге болады:

1.

2. құрылымы лента тәріздес болады;

3. сирелген болып табылады.

Жүйе шешiмiне тиiмдi итерациялық әдiстерді қолдануға болады.

Анық шартты анықталмаған сұлба орнықты болатыны дәлелдеген.

k = k(x, y, u) бұл әдіс оңай жағдайда жалпылайды, егерт теңдеу туындаса. Бұдан басқа, бұл әдiс шектi шарттардың жағдайына қорыта алады. (9.3 ) осы жағдайда функционалға шекаралар бойынша тиiстi интегралдар қосылады, ал (9.5 ) - беттер бойынша сомасы қосылады.

Толығырақ бұл сұлба туралы [19.2 ]беттен оқып шығуға болады.

Өздік есептер үшін тапсырмалар.

1. Кортевега-Де Фриза теңдеуі

Кортевега-Де Фриза теңдеуі (қысқаша КДФ) – математикалық физика теңдеуінің

Өзін өзі бақылауға арналған тапсырмалар:

1. Гамильтон қағидасының негізі неде?

2. Газдық динамика есептерін шешуге арналған ваиациялық сұлбалар жайлы айтып беріңіз

3. Есептерді өзіндік шешіп кқріңіз.

 

 

4. Лекция: Газды динамиканың теңдеулерiнiң сандық шешiмiнiң әдiстерiне кiрiспе:

Дәріс алғашқы кітапты оқығанда қажет емес. Бұл дәрісте кейбір жиі кездесетін сандық әдістер теңдеулерінің газды динамика қолданулары келтіріледі.

 

Туындылардың бөлiндiлерiндегi теңдеулердiң шешiмiнiң айырма әдiстерi қарастырылған алдыңғы дәрiстердегі мысалда сызықты есептермен немесе қасиеттері жақсы зерттелген сызықты емес теңдеулердiң бос тұрулары жеткiлiктi болған. Нақты есептеуiш тәжiрибедегi мұндай есептер күрделiрек сызықты емес жүйелердi шешу әдiстерiнің жан-жақты зерттеуi үшiн тесттермен әдетте қызмет көрсетедi. Сандық әдістердің дәстүрлі объектісі болып тұтас орта механика(ТОМ) теңдеуі болып табылады. Бұның негізгі себебі үшеу. Біріншісі-барлық ТОМ-ң модельдері әлдеқашан ереден белгілі, олар жақсы зерттеліп және ғылыми классикның бір бөлшегі болып келеді. Екіншісі –ТОМ-ң математикалық моделі сызықты емес. Әдеттң түзетілген теңдеулердің қолдану облысы кең емес. Үшіншісі –ТОМ-ң XX ғасырлардан бастап қызығушылығы, авиацияның өте қарқынды тез дамуымен, ядролы ғылыммен және әр түрлі елдердегі ғарыштық программалардың өсуінен болды. Бұл кітапта ТОМ-ң ең қарапайым газдық динамика теңдеулерімен шекелеміз. Бұл дәрістің басты идеясы –жоғарыда көрсетілген ойлармен және есептеуіш математика әдісін нақты есептерде қолдану.

 

4.1 Бiр өлшемдi газ динамика теңдеулердi жазу түрі.

Сұйықтармен газдардың қасиеттерін қарастырудағы математикалық модельдерді құру негізінде тұтас орта ұғымы жатыр. Ортаның жеке бөлшектерден тұратындығы(малекула, ион, атом, электрондар) және олардың арасындағы қашықтық өз өлшемдерінен үлкен екенін малекулалақ физикадан белгілі. Еркін қозғалған бөлшек ұзындығы 1 (екi соқтығысулардың арасындағы бөлшек өтiлген қашықтық) бірлік көлемде бөлшек неғұрлым аз, неғұрлым көп болуы орта тығыздығы соғұрлым көп болуына әкеледі. Сұйықтармен газдардың механикасында бірлік көлемде көп бөлшектер болатын орта қарастырылады (Авагадро санынан көп бөлшек). Авагадро –бір граммдғы бөлшек саны. Ол .

Мұндай ортада әрбір бөлшектің жеке-жеке сипаттамасын қарастырмай, кейбір ортақ сипаттамаларды ғана қарастыруға болады.

Жуықтаудың қолданылғыштығының есептiк белгiсiмен тұтас орта теңсiздiк мүмкiн қызмет ету. Тұтас ортаның жуықтауының есептік критериі мына теңсіздікпен өрнетеледі: , мұндағы L-кеңістік өлшеміне тән есеп(мысалы, сыртқы айнала ағудағы газ ағымының дене өлшемi). Газдың қалыпты жағдайында см, сондықтан қойылған шарт 1 см өлшемді денеге жеткілікті дәлдікпен орындалады. Тұтас орта ұғымы өз бастамасын үзіліссіз деформацияға ұшырайтын субстанция деп қарастырған Эйлерден алады. Газ динамикасы теңдеуіне қарамастан (бұл тақырыпқа өте көп кітаптар арналған [14.1], [14.2], [14.3]) оны соңғы түріне келтіреміз.

Газ динамикасының теңдеулерiнiң бiр өлшемдi жүйесiн Эйлерлік (недивергентная) түріне келеді:

(4.1)
мұндағы e- меншікті қуат, - тең меншікті ішкі энергия, u-газ жылдамдығы, -орта тығыздығы, p-қысым, t-уақыт, x-декарттық координата. Бұл теңдеу жүйесін меншікті тундыларын матрицалық(сипаттамасын) түрде келтіруде болады

Мұндағы - вектор-баған, - 3 x 3-шi квадрат матрицасы.

Жүйе мына түрде тұйықталады

идеал газы үшін

болады.

Мұндағы -шексіз тұрақты, тұрақты қысымда газдың жылу сыйымдылығына тең және тұрақты адиабаталық қысымға тең көлем.

Матрицалық түрде жазылған (4.2) температура функциясында қысым(немесе меншікті ішкі энергиясы) және қысымы бар екені ескерілген демек

Формула қорытындысымен айналыспай (жай алгебралық түрлндірулермен жүзеге асады) энергия түрлерінің басқа жазулары бар екен деп жоғарыда келтірілген теңдеуге дұрыс

аламыз

мұндағы -адиабаталық дыбыс жылдамдығы

-энтропия. Ол, соңғы формуладағыдай, идеал газдың бөлшегiнiң траекториясын сақтайды, яғни теңдеудiң траекториясында

Газ динамикасы теңдеулердi дивергент түрі интегралдық түрде жазған кезде тиiстi сақталу заңдарын алады. Егер осыдан кейін шекті ауыстырым жасаса, онда диференциалдық теңдеу

(4,3)

 

болады.

 

немесе матрицалық түрде

Бұл теңдеудің интегралдық түрі Гаусс – Остроградский теоремасын қолданғаннан шығады.

мұндағы - интегралының t, x жазықтығындағы тұйық облысының шегі. Мұнда -сәйкесінше газдың тығыздығы, жылдамдығы және қысымы. Механикада әр-түрлі ортада эйлерлік және лагранжтың орта жайлы сипаттамалары қолданады. Бірінші жағдайда бақылаушы жылжымайтын болып саналады, мысалы өзен жағасында тұрған адам. Сәйкесінше есептеу торы жылжымайтын болады(белгiленген эйлер торы). Екінші жағдайда бақылаушы ортамен бірге жылжиды деп есептейміз, мысалы өзен ағысымен жүзіп келе жатқан қайықта отыруы. Бұл жағдайда лагранждық есептеу торы ортаның бөлшектерімен бірге қозғалады.

Лагранж теңдеуі бiр өлшемдi газ динамикасы теңдеуі сияқты болады

мұндағы