Иммунизация с использованием выпуклости

Эквивалентным способом расчета дюрации является запись исходного уравнения в виде

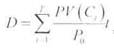
где Р₀ - текущий рыночный курс облигации;

^' (С/) ~ приведенная стоимость потоков платежей по облигации при ставке дисконтирования, равной доходности к погашению; 7 ^ срок погашения облигации.

Вначале приведенная стоимость каждого платежа PVyCA

выражается как некоторая доля рыночного курса Р₀, затем эти доли умножаются на величины соответствующих периодов времени до наступления платежей и, наконец, полученные результаты суммируются и получается значение показателя дюрации.

Рассмотрим расчет дюрации на примере. Пусть имеется облигация с ежегодным купонным платежом 80 ден. ед., сроком до погашения 3 года и номиналом 1000 руб. Текущий рыночный курс равен 950,25 руб., доходность к погашению 10%.

Таблица 5 Расчет дюрации

Время до наступлении n.ia i ежа	Сумма платежа, руб.	Ставка приведении 1/(1+0,1)'	Приведенная стоимость платежа, руб (2) х (3)"	Приведен паистоимость платежа, умноженная на время (4)х (1)
I	80 1080	0.9091 0.8264 0.7513	72.73 66.12 811.40	72.73 132.24 2434.20
Итого:	950.25	2639.17

Через 1 год будет получена часть рыночного курса облигации, равная

72 71

' =0.07653. 950,25

через 2 года

-^1^ = 0,06958.

950,25

через 3 года

«1Ь*= 0,85388

950.25

В сумме эти доли дают единицу: 0,07653 + 0,06958 + 0,85388 = 1, что и позволяет их использовать в качестве весов при вычислении взвешенного среднего. Взвешенное среднее платежей по облигации равно: (1 0,07653) + (2 0,06958) + (3 0,85388) = 2,78 года.

Таким образом, для вычисления дюрации каждый вес нужно умножить на соответствующий отрезок времени до наступления данного платежа и затем полученные значения сложить.

Для бескупонной облигации, с которой связан только один платеж, поскольку PV(C\) = /> , то уравнение дюрации принимает вид

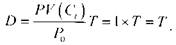
Для всякой купонной облигации дюрация всегда меньше периода времени до погашения j . Так как максимальное значение, которое

может принимать t, равно у , и каждое t умножается на вес ~ ^< ' ,

'о

то следовательно, /) < у .

Одно из следствий теоремы оценки облигаций заключается в том, что облигации, имеющие одинаковые сроки погашения, но различные купонные платежи, могут по-разному реагировать на одно и то же изменение процентной ставки, т.е. курсы этих облигаций могут меняться по-разному при заданном изменении процентной ставки. Однако, облигации с одинаковой дюрацией в этом случае реагируют сходным образом. Процентное изменение курса облигации связано с ее дюрацией следующей формулой:

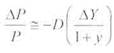
где дуэ - изменение курса облигации; р - начальный курс облигации;

ду - изменение доходности к погашению облигации; V - исходная доходность к погашению. Величина

называется модифицированной продолжительностью, она показывает, насколько изменится цена облигации при изменении ставки Доходности по облигации на один процент, т.е.

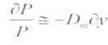
Облигация, представленная в табл. 5 имеет дюрацию 2,78 и доходность 10%. Модифицированная продолжительность данной облигации равна:

Таким образом, при изменении доходности к погашению на 1%, т.е. до 1 1%, цена (курс) облигации изменится приблизительно на 2,53% и будет равен:

Р - АР = 959.25 - 950,23 х (), 0253 = 926,49 руб.

Используя ставку дисконтирования 11% можно точно вычислить курс, который в данном случае будет равен:

80 80I080

~7Л⁺(1 1 1)' ⁺(и!Тз =72,07 + 64,93 + 789,69 = 926,69 руб.

Фактическое изменение курса при этом составит

Таким образом, продолжительность достаточно точно измеряет колебания цены в ответ на небольшие изменения доходности. Поскольку зависимость между изменениями доходности и изменениями курса является выпуклой, а не линейной, использование уравнения (3.11) приводит к занижению нового курса, соответствующего либо возросшей, либо понизившейся доходности облигации.

Более точную оценку удается получить с использованием показателя выпуклости.

Степень крутизны (выпуклости) кривой РуУ) (см рис. 19) не

одинакова для различных облигаций. Она, среди прочего, зависит от величины купонных платежей, срока обращения облигации и ее текущего рыночного курса.

Выпуклостью облигацииназывается показатель, измеряющий

степень выпуклости зависимости цены облигации от ее доходности: Р(у) ■

Выпуклость в денежном выражении представляет собой чувствительность показателя продолжительности облигации к изменению ставки доходности и рассчитывается на основании второй производной функции цена - доходность:

Просто выпуклостью называется величина

I I д²Р

W= — W_d= г

2Р 2Р дуг '

Последний показатель позволяет уточнить влияние изменения доходности на цену (курс) облигации.

Используя разложение функции Р(у) в ряд Тейлора, получим формулу квадратичной аппроксимации зависимости цены от доходности:

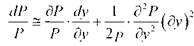
или, поделив обе части на р , получим

^d-^ = -D_m(dy) ₊ W{dy)²

т.е

При возрастании доходности до 11% использование показателя выпуклости позволяет получить более точную оценку изменения цены облигации.

Рассчитаем выпуклость облигации для предыдущего примера:

На основании формулы (3.14) получим, что курс облигации изменится приблизительно на:

Реальное изменение курса -2,48%, изменение курса с использованием дюрации -2,53, то же, но с использованием выпуклости

-2,48%.

Таким образом, использование показателя выпуклости позволяет получить более точную оценку изменения курса облигации при изменении доходности на 1%.

Единицей измерения выпуклости является промежуток времени между купонными выплатами в квадрате. Для приведения данного показателя к годовой размерности, необходимо разделить значение выпуклости на число купонных выплат в год, возведенное в квадрат. Например, для купонной облигации, номинальной стоимостью 100 ден. ед.. сроком обращения 1 год и ежеквартальной выплатой купона в размере 22,44 руб., ценой на момент выпуска 139,44 ден. ед. и доходностью к погашению 40% годовых показатель выпуклости равен 6,01, или 6,01/ 16 = 0,375 лет в квадрате.

Если на рынке существует достаточное число облигаций с различными сроками погашения, то портфель облигаций всегда можно подобрать таким образом, чтобы денежные потоки, которые он обеспечивает, в точности соответствовали потребностям инвестора как по срокам, так и по объемам. Такой подход формирования портфеля называют стратегией подбора денежных потоков, которая вместе с рассмотренной выше стратегией иммунизации является примером пассивных стратегий управления портфелем инструментов с фиксированным доходом. И в том, и в другом случае цель, преследуемая при формировании портфеля, состоит в том, чтобы максимально обезопасить портфель от неблагоприятных изменений рыночной доходности, при этом пассивный подход построен на предположении о невозможности прогнозирования будущих процентных ставок.

Применение как активных, так и пассивных стратегий управления портфелем облигаций имеет свои недостатки. В случае пассивных стратегий - доходность портфеля сознательно ограничивается с целью снижения риска. При активном подходе - велик риск потерь, связанных с неверным прогнозом будущих процентных ставок. Наиболее эффективными по этой причине являются методы, объединяющие в себе черты одновременно и активного, и пассивного подходов, одним из таких методов является условная иммунизация. Упрощенно, условная иммунизация состоит в формировании портфеля, продолжительность которого несколько больше (если прогнозируется снижение процентных ставок) или меньше (если прогнозируется повышение процентных ставок), чем продолжительность планового горизонта. Она представляет собой динамическую стратегию, цель которой состоит в том, чтобы гарантировать определенный минимальный уровень доходности, одновременно пытаясь с помощью приемов активного управления достичь максимума эффективности. Таким образом, в каждый момент времени необходимо оценивать на основании текущей структуры процентных ставок фактическую и минимально необходимую для обеспечения иммунизации стоимость портфеля. Если фактическая стоимость с запасом превышает этот минимальный уровень - есть

возможность продолжать использование активных методов, если нет -портфель должен быть немедленно иммунизирован, что позволяет избежать потерь.