Базовая модель Марковица

 

Модель, согласно которой инвестиции оцениваются исключительно по двум параметрам - ожидаемой доходности и риску, измеряемому как величина стандартного отклонения доходности, позволяет сформулировать единое правило формирования портфеля, которому следуют все инвесторы: независимо от индивидуальных предпочтений все инвесторы стремятся сформировать эффективный портфель, т.е. такой, который обеспечивает минимальную степень риска для выбранного уровня дохода, либо максимальный ожидаемый доход при заданной степени риска. Этот подход и сама задача поиска эффективного портфеля называется моделью Марковица.

Основными постулатами теории Г. Марковица являются следующие:

1) рынок состоит из конечного числа активов, доходности которых для заданного фиксированного периода считаются случайными величинами;

2) инвестор, располагая статистическими данными в совместных распределениях доходностей по всем активам, может получить оценку ожидаемых (средних) значений доходностей и их попарных ковариаций;

3) инвестор может формировать любые допустимые портфели для данной модели, при этом доходности портфелей также являются случайными величинами;

4) портфели сравниваются по двум критериям: математическому ожиданию доходности (как мере доходности) и по дисперсии (как мере риска);

5) инвестор не склонен к риску, т.е. из двух портфелей с одинаковой доходностью он выбирает портфель с меньшим риском;

6) индивидуальные предпочтения инвестора задаются сверткой критериев в один критерий, который является некоторой функций полезности инвестора. Функция полезности зависит только от доходности и риска.

В модели Марковица доходность портфеля рассчитывается как взвешенная по объемам инвестиций доходность каждого, входящего в портфель, актива

Ожидаемая доходность портфеля ц определяется по формуле математического ожидания суммы случайных величин:

 

Таким образом, ожидаемая доходность инвестиционного портфеля - это средневзвешенная по долям инвестиций ожидаемая доходность каждого из активов, входящих в портфель.

Дисперсия доходности портфеля рассчитывается как дисперсия суммы случайных величин:

Полагая

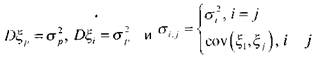
получаем

Если о^- - коэффициент ковариации показателей доходности двух ценных бумаг, то

где о",, гт, - стандартные отклонения значений доходности от среднего

значения;

р_р - коэффициент корреляции случайных величин £, и <^₂.

Таким образом, формулу для расчета стандартного отклонения портфеля, состоящего из двух активов, можно представить в виде:

Следовательно, общий риск портфеля зависит от величины риска активов, входящих в портфель (о",), доли каждого из активов в

портфеле (х,) и коэффициент корреляции \Р_]2)-

Эффект диверсификации, или распределения, инвестиций между различными инструментами и объектами, состоит в том, что, выбирая объемы инвестиций в различные активы, инвестор может регулировать

рискованность портфеля, т.е. выбирать такую величину о_р из возможных,

которая отвечает его предпочтениям.

Возможности по снижению риска портфеля зависят от тесноты связи

между доходностями различных инвестиционных решений р_р .

Величина коэффициент корреляции двух случайных величин может изменяться в пределах от -1 до 1. Равенство р_|2 = -1 означает совершенную отрицательную взаимосвязь между доходностями двух активов (если доходность одного актива увеличивается, то доходность

второго пропорционально снижается и наоборот). При р = 1 оба актива характеризуются совершенной положи 1ельной взаимосвязью (любое увеличение доходности одного из них сопровождается

пропорциональным увеличением доходности второго). Если р_|2 = 0, то

доходность одного актива никак не связана с доходностью второго. Пусть целью инвестора является выбор портфеля из двух активов,

т.е. требуется определить такие х и х₂, чтобы величина риска портфеля

о была наименьшей. Задача решается аналитически.

При р_|2 = - 1 портфель минимального риска определяется из условия:

При л^-, =х* и а'₂ =1 —А'* риск портфеля равен нулю, что легко проверить.

Риск такого портфеля равен

Когда р_|2 = 0, портфель наименьшего риска выбирается следующим образом:

что меньше, чем риск каждого из отдельно взятых активов <у и о\ . Можно показать, что при некоррелированных ценных бумагах ( р_ц = О,

если i /') при росте числа их видов в портфеле риск портфеля стремится к нулю при п —>

При р = 1 оптимальный портфель выбирается из условия:

 

В отличие от случая, когда р_р -1 и оптимальные объемы инвестиций в каждый актив были положительными, здесь мы имеем либо v* либо 1-х*

Риск такого портфеля равен нулю

 

меньше нуля, причем, если _х* < 0, то (1-х*) > 1 и наоборот. Отрицательный объем инвестиций означает короткую продажу, т.е. когда продается актив, взятый в долг с обязательством последующего возврата.

Следовательно, в случае положительной корреляции между доходностями двух активов, необходимо коротко продать один из активов и инвестировать все имевшиеся и вырученные за счет короткой продажи средства во второй актив.

Полученные результаты позволяют сделать следующие выводы: чем больше степень статистической взаимосвязи между доходностями двух активов, тем большие возможности по снижению риска путем комбинации инвестиций в эти активы (т.е. формирования портфеля), следовательно, более эффективна диверсификация, предпринимаемая с целью снижения риска.

Чем меньше величина р (чем ближе она к -1), тем меньшего

уровня риска можно достичь, причем при p_l2 = -1, как было показано выше, существует портфель с нулевым риском. Данный факт положен в основу хеджирования - деятельность по снижению риска, когда инвестор, для того чтобы обезопасить себя от возможных потерь, связанных с инвестированием в некоторый актив, одновременно инвестирует в другой актив, доходность которого негативно коррелирует с доходностью первого.

В теории портфеля Г. Марковица ставится задача об оптимальном портфеле. Получающаяся при этом оптимизационная задача является многокритериальной. В ее решении используются различные методы. Назовем лишь три наиболее распространенных подхода:

а) осуществляется поиск не наилучшего сразу по всем критериям,
а эффективных портфелей, т.е. не улучшаемых сразу по всем критериям;

б) какой-то один критерий объявляется главным, по всем остальным
критериям задаются пороговые значения и они становятся
критериальными ограничениями (например, минимизируется риск при
условии, что доходность должна быть не ниже определенной величины);

в) все критерии каким-либо образом сворачиваются в один.

Оценкой портфеля называют пару чисел (р(л"),о~ (х)), которую можно изобразить точкой Q_n на плоскости y/.i,<jj (рис. 8). Плоскость (/-/,о~~ J называется критериальной. Множество всех оценок допустимых

портфелей, т.е. множество пар (р,<т ) называют критериальным

множеством. Если критериальное множество не сводится к одной точке, то возникает проблема выбора.

Пусть 7Г₀ - некоторый портфель, a Q₀ =Ш,<т₀ I - оценка для этого

портфеля. Критериальную плоскость можно разбить на четыре квадранта (рис. 8).

 

 

Рис. 8. Критериальная плоскость и соотношение портфелей

 

Если какой-то другой портфель я, имеет оценку в четвертом

квадранте, то я, лучше я₀, поскольку //, > /л₀ и erf < о\. Если оценка

для я, попадает во второй квадрант, то я, хуже я₀, так как /л, < /;₍₎ и

от," > о"₀, причем для обоих этих квадрантов хотя бы одно из неравенств

в приведенных парах - строгое. Если же оценка Q портфеля я, находится внутри (не на пунктирах рис. 8) первого и третьего квадрантов, то имеются два таких портфеля, у которых один показатель лучше, чем у другого, зато второй - хуже.

Портфель я₀ называют эффективным во множестве допустимых портфелей, если не существует лучший портфель, т.е. не существует портфель я,, такой, что /./, > //<, и <т~ < а~. Эффективный портфель -

это портфель, не улучшаемый сразу по двум критериям.

Свойство эффективности наглядно представлено на рис. 9. Для некоторого портфеля по его оценке строится "четвертый квадрант". Портфель эффективен в том и только в том случае, когда в этом квадранте

нет других допустимых портфелей. На рис. 9 портфель я₀, имеющий

оценку Q_Q эффективен, а портфель я, с оценкой Q не эффективен,

так как существует портфель я , с оценкой Q₀, который лучше я, сразу по двум критериям.

Рис. 9. Геометрическое представление эффективного портфеля Q₀ и эффективной границы Q₀ S множества

Эффективные портфели данного множества допустимых портфелей составляют эффективную границу множества (эффективные портфели могут лежать только на границе). Эффективные портфели называются также оптимальными по Парето, а их множество - множеством Парето (Вильфредо Парето - итальянский экономист (1948-1923), один из первых исследователей многокритериапьных оптимизационных задач в экономике).

Определение множества эффективных портфелей представляет собой первый этап в решении проблемы выбора наилучшего портфеля. Одним из методов ее решения является нахождение портфелей, "экстремальных" по одному из критериев при заданном значении другого

критерия. Зафиксировав уровень доходности /./„ , можно искать

портфель с этим уровнем доходности и с минимальным риском. Для разных уровней доходности будут получены свои значения минимального риска. Такие портфели называют минимальными по риску, а их оценки составляют минимальную границу критериального множества.

На рис. 10 изображен минимальный по риску портфель с оценкой

Q₀ и уровнем доходности /i₀. Оценки остальных портфелей с этим

уровнем доходности находятся на вертикальном отрезке Q₀Q_t (сечение критериального множества). Минимальная граница представлена

 

 

 

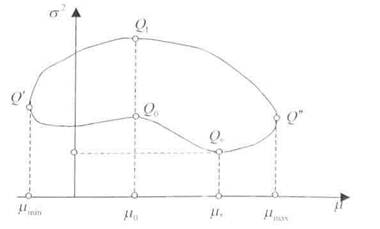
Рис. 10. Геометрическое представление минимальной границы Q'QjQ„Q' критериального множества кривой Q'QqQ*Q"

Эффективная граница Q,,Q" является частью минимальной границы. Как показал Г. Марковиц, минимальную границу

на плоскости (/./, о~ j можно представить графиком непрерывной функции, который задает минимум риска при заданной доходности:

°² =./;,„„ (я).

Ценность минимальной границы и приведенного результата Марковица состоит в том, что становится возможным реализовать один из подходов к решению многокритериальной оптимизационной задачи - задавшись значением доходности, искать портфель с минимальным риском. Непрерывность минимальной границы позволяет это сделать.

В модели Марковица допустимыми являются только стандартные портфели (без коротких позиций), т.е. при которых на представляющий их вектор накладываются два ограничения:

Основное

и неотрицательности

х, > О

для всех активов a_t.

Особенностью модели Марковица является ограниченность доходности допустимых портфелей, т.е. доходность любого стандартного портфеля не превышает наибольшей доходности активов, из которых он построен. Таким образом, если

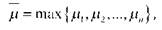
где j.i - максимальная из доходностей активов, составляющих портфель, то /( < /л ■

Это равенство следует из неотрицательности компонент а~. и

основного ограничения / ,^х, ~ '.

Критериальное множество для модели Марковица в двумерном случае представляет собой дугу параболы между точками Q и Q,, соответствующим оценкам двух активов (рис. 11).

На плоскости (;;,ст) возможно наглядное представление семейства критериальных множеств, соответствующих различным значениям коэффициента корреляции р. На рис. 11 критериальные

множества при ре[-l;l] представлены частями гипербол, сплошь

заполняющих треугольник Q_x Q,Q~, , границы которого образованы критериальными множествами, соответствующими крайним значениям р = ±1.

Рис. 11. Критериальные множества в модели Марковица при различных значениях р на плоскости (/./, О )

Двумерные модели обладают тем свойством, что критериальное множество представлено линиями на плоскости и границы этого множества совпадает с ним самим. Если активов больше двух, то критериальное множество будет "двумерным", т.е. оно будет содержать и внутренние точки. Полученные результаты для модели из двух активов могут быть использованы и в общем, т.е. в многомерном случае для п активов, при этом вместо двух активов рассматриваются два портфеля, состоящих из п активов. Таким образом, многомерная модель сводится

к двумерной подмодели. Важным является, что в многомерном случае критериальное множество обязательно выпукло вниз и его минимальная граница есть выпуклая кривая, следовательно, риск может быть снижен за счет формирования некоторого портфеля. Марковиц показал, что на

плоскости ifu,(7j минимальная границы критериального множества

в многомерной модели представлена конечным числом кусков парабол, более того, вся полная граница критериального множества на плоскости

yf-i, о"| состоит из кусков парабол. Типичный вид критериального

множества в модели Марковица представлен на рис. 12. В современной финансовой литературе принято обратное правило: по оси абсцисс отмечается риск, а по оси ординат - доходность, что приводит к преобразованию изображения критериальных множеств (рис. 13).

Рис. 12. Критериальное множество в Рис. 13. Современное представление
модели Марковица в многомерном критериального множества

варианте допустимых портфелей

Полное устранение риска в многомерном варианте возможно только при наличии безрискового актива. Хотя теоретически такое устранение возможно, например, в случае, когда коэффициент

корреляции р = ±\ , на практике достижение этого невозможно, поскольку в реальности не бывает активов с единичным коэффициентом корреляции.

Математически модуль Марковица формулируется так - найти такие

пропорции распределения средств между активами х_],х₂,...,х_п (где х.

- доля средств, инвестируемых в / -й актив), чтобы риск портфеля о ,,

при заданном уровне доходности ц_р был бы минимальным, и сводится к решению следующей оптимизационной задачи:

при ограничениях:

где /.i_р - заданный уровень средней доходности, а

Наличие ограничений неравенство значительно усложняет решение этой оптимизационной задачи. Тем не менее существует большое число эффективных алгоритмов ее решения. Поиск аналитического решения осуществляется с использованием множителей Лагранжа и обратной матрицы (подробно рассмотрено в [29]).

В общем случае модель Марковица представляет собой задачу квадратичного программирования и решается стандартными методами. Наиболее сложная проблема, связанная с ее практическим использованием - подготовка исходной информации об ожидаемой доходности, стандартном отклонении и коэффициентах ковариации финансовых активов.