Поток напряжённости. Теорема Гаусса для электростатического поля в вакууме

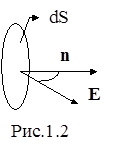
Элементарным потоком напряжённости электрического полясквозь малый участок площадью dS поверхности, проведённой в поле, называется скалярная физическая величина

dN = 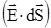= EdScos( 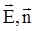) =E_ndS = EdS_^,

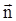где — вектор напряжённости электрического поля на площадке dS, - единичный вектор нормали к площадке dS, 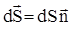-вектор площадки, Е_n = Ecos( 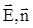) - проекция вектора на направление вектора 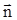, dS_^ = dScos( 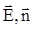) - площадь проекции элемента dS поверхности на плоскость, перпендикулярную вектору (рис.1.2).

Теорема Гаусса: Поток напряжённости электростатического поля в вакууме сквозь произвольную замкнутую поверхность пропорционален алгебраической сумме электрических зарядов, охватываемых этой поверхностью:

,

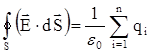где все векторы 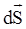направлены вдоль внешнихнормалей к замкнутой поверхности интегрирования S, которую часто называютгауссовой поверхностью.

Приведем несколько примеров результата расчета модуля напряженности электростатического поля в вакууме при помощи теоремы Гаусса:

1. Поле заряда q, равномерно распределенного по поверхности сферы радиуса R:

 

r < R E = 0

.

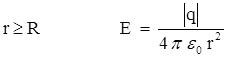Здесь r – расстояние от центра сферы до точки, в которой определяется напряженность поля.

2. Поле заряда q, равномерно распределенного по объему шара радиуса R с объемной плотностью: .

r < R ,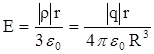

.

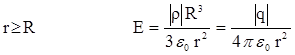Здесь r – расстояние от центра шара до точки, в которой рассчитывается напряженность поля.

3. Поле заряда, равномерно распределенного по бесконечной плоскости с поверхностной плотностью σ:

.

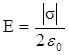4. Поле заряда, равномерно распределенного по бесконечной нити с линейной плотностью τ :

.

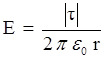Здесь r – расстояние от нити до точки, в которой рассчитывается напряженность поля.