Глава I. Основные понятия и формулы теории вероятностей.
А.В. Ряднов, В.В. Трубаев, Т.В. Меренкова
Теория вероятностей
Учебное пособие
Москва - 2013
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»
Кафедра «Высшая математика»
А.В. Ряднов, В.В. Трубаев, Т.В. Меренкова
Теория вероятностей
Рекомендовано редакционно-издательским советом университета в качестве учебного пособия для студентов технических специальностей ИТТСУ
Москва - 2013
УДК 519. 2
Р 98
Ряднов А.В., Трубаев В.В., Меренкова Т.В. Теория вероятностей: Учебное пособие. – М.: МИИТ, 2013. –191 с.
Учебное пособие представляет собой единое методическое руководство, включающие в себя доказательство основных формул теории вероятностей, охватывающее основные разделы теории вероятностей. Оно содержит типовые задачи с подробным решением. В конце пособия предлагаются задачи для самостоятельной работы и типовые расчёты. Студентам эта книга вполне заменит репетитора, а преподавателю сэкономит время на подготовку лекционных, практических и домашних заданий. Пособие предназначено для студентов всех технических специальностей ИТТСУ МИИТа.
Рецензенты: к.ф.-м.н., доцент кафедры «Прикладная математика» МИРЭА Воронцов А.А.; к.ф.-м.н., доцент кафедры «Математический анализ» МИИТ Деснянский В.Н.
© МИИТ, 2013
Оглавление
Глава 1. Основные понятия и формулы теории вероятностей………………………………………….. 5
§ 1. Предмет теории вероятностей. Случайные
события ………………………………………. 5
§ 2. Вероятность случайного события …………... 8
§ 3 Алгебра событий …………………………….. 12
§ 4 Формула сложения вероятностей …………… 17
§ 5 Аксиоматический подход к теории
вероятностей ………………………………… 19
§ 6 Классическая схема теории вероятностей …. 24
§ 7 Геометрические вероятности ……………….. 26
§ 8 Условная вероятность. Независимость
случайных событий …………………………. 29
§ 9 Формула полной вероятности. Формулы
Байеса ……………………………………….... 39
§ 10 Комбинаторика ………………………………. 42
§ 11 Схема Бернулли ……………………………..... 49
§ 12 Вероятности 
при больших значениях n.
Глава 2. Случайные величины и их характеристики62
§ 1 Случайная величина и её функция
распределения .................................................. 62
§ 2 Дискретные случайные величины ................. 67
§ 3 Непрерывные случайные величины .............. 70
§ 4 Функции от случайной величины .................. 78
§ 5 Системы случайных величин ………………. 81
§ 6 Независимые случайные величины ………... 89
§ 7 Математическое ожидание случайной
величины …………………………………….. 94
§ 8 Дисперсия случайной величины ………….... 109
§ 9. Корреляционный момент и корреляция
случайных величин ……………………………. 113
Глава 3. Закон больших чисел и центральная
предельная теорема……………………… 119
§ 1 НеравенствоЧебышева ……………………... 119
§ 2 Закон больших чисел ………………………... 123
§ 3 Центральная предельная теорема Ляпунова и
её следствия …………………………………129
Задачи по теории вероятностей …………………… 138
Индивидуальные задания № 1 по теории
вероятностей …………………………………………… 153
Индивидуальные задания № 2 по теории
вероятностей …………………………………………... 166
Таблица значений функции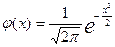 
…….. 183
Таблица значений для функции
................................................... 185
Степени числа e ....................................................... 188
Таблица значений функции 
………………..... 189
Глава I. Основные понятия и формулы теории вероятностей.