Вычисление абсолютной и относительной погрешности

Наиболее вероятное значение функции у, т.е. результата косвенного измерения получается при подстановке в (1.17) средних значений аргументов

у_изм = f( ), (1.18)

Поскольку каждая из величин (где k=1,2, …, n) определена с погрешностью, то величина у_изм также будет найдена с некоторой погрешностью. В теории погрешностей (выходящей за рамки данного пособия) показано, что эта погрешность вычисляется по формуле:

(1.19)

где – частная производная функции, x_k аргументу, вычисленная при среднем значении ;

– абсолютная погрешность прямого измерения.

Относительная погрешность:

(1.20)

Формула (1.20) является общей и может быть упрощена для частного случая, когда аргументы входят в функцию в виде сомножителей

,

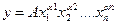где А – любой постоянный множитель;

α – показатель степени,

тогда можно записать

(1.21)

Формула (1.21) более удобна для вычислений, поскольку относительные погрешности прямых измерений уже определены, однако, если функция представлена не произведением аргументов, а иной зависимостью, то необходимо использовать (1.20).

Пример. Пусть определяется плотность тока через проводник

где D – диаметр проводника;

I – величина тока.

В эту формулу все аргументы входят в виде сомножителей. Рассчитаем относительную, а затем абсолютную погрешность. В соответствии с (1.20):

Число π здесь не считается постоянным, т.к. в зависимости от смены округления оно будет различным (Δπ – погрешность, обусловленная округлением).

Найдем производные:

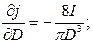
Тогда

Следовательно:

Заметим, что последнюю формулу можно было записать сразу на основании (1.21).

Предположим, что ток измеряется амперметром, а диаметр провода микрометром. Результаты наблюдений представлены в форме таблицы (табл. 1.4).

 

Обработка результатов прямых испытаний проводится по правилам, изложенным в п. 1.2.

Таблица 1.4

Результаты наблюдений

Номер наблюдения	D	∆D	I	∆I
мм	мм	мA	мA
	6,40	- 0,020	20,8	+ 0,12
	6,42	0,000	20,4	- 0,28
	6,41	- 0,010	20,7	+ 0,02
	6,43	+ 0,010	20,9	+ 0,22
	6,44	+ 0,020	20,5	- 0,18
	6,42	0,000	20,8	+ 0,12
	6,41	- 0,010	20,5	- 0,18
	6,43	+ 0,010	20,8	+ 0,12
	6,41	- 0,010	20,9	+ 0,22
	6,43	+ 0,010	20,5	- 0,18
	6,42		=20,68

 

Для наблюдений величины силы тока получим:

=0,13 мм; =0,067 мА; =0,048 мА;

=0,16 мА; =0,77%.

Для наблюдений диаметра проводника получим:

=0,0090 мм; =0,027 мм; =0,0048 мм; =0,011 мм; =0,17%.

Для того чтобы погрешностью ∆π∕π можно было пренебречь необходимо число π взять с четырьмя значащими цифрами:

π = 3,142.

Тогда ∆π<0,0005 и ε_π < 0,02%.

В этом случае относительная погрешность косвенного измерения:

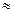ε_j = =0,84% 0,8%.

Плотность тока = 6,306 мА/мм²

Абсолютная погрешность:

.

Результат измерения: j =(6,306±0,050) мА/мм²;

ε_j=0,8 % ; Р=0,95.

В заключение отметим, что формулы (1.17), (1.18), (1.19) справедливы только в том случае, когда все аргументы независимые и измерены независимыми методами.