Действие магнитного поля на заряженные частицы

На частицу с электрическим зарядом q, движущуюся в магнитном поле со скоростью 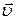, направленной произвольным образом по отноше­нию к вектору магнитной индукции , действует сила Лоренца

= q[ , ].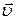

В скалярном виде величина силы Лоренца может быть представлена формулой:

F _Л = quBsina , (2.8)

где a – угол между векторами 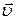и (рис. 1.1).

Сила Лоренца влияет на направление вектора скорости и сообщает частице нормальное ускорение.

Радиус окружности R (рис. 2.3), по которой движется частица, можно найти из соотношения:

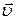, если ^ .(2.9)

Период обращения частицы

. (2.10)

Если вектор скорости 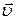заряженной частицы составляет угол a с направлением вектора однородного магнитного поля, то частица движется по винтовой линии, навивающейся на линию магнитной индукции поля. Радиус R и шаг h винтовой линии (при u<<c):

R=musina /(|q|B), (2.11)

h=2pmucosa/(B|q|). (2.12)

2.3.Работа сил магнитного поля

Элементарная работа dА, совершаемая силой Ампера d _А при малом перемещении d в магнитном поле элемента тока Id

 

dA = = = = I dF_m, (2.13)

где dF_m - магнитный поток сквозь поверхность, которую прочерчивает элемент проводника при его перемещении.

Работа перемещения проводника с токомв постоянном магнитном поле

A = I∙F_m, (2.14)

где F_m – магнитный поток сквозь поверхность, которую прочерчивает весь проводник при его полном перемещении.

Работапри перемещении в магнитном полезамкнутого контура с постоянным током I из положения 1 в положение 2

A₁₂ = I (Ф_m2 –Ф_m1) =IDF_m, (2.15)

где Ф_m1 и Ф_m2 – магнитные потоки через поверхность контура с током в начальном и конечном положениях.

Если в магнитном поле перемещается катушка, имеющая N витков, то работа может быть определена

A₁₂ = I DY₁₂ = INDФ_m12,

где DY₁₂ – изменение потокосцепления контура при его перемещении.

Все приведенные соотношения справедливы, если значения сил токов в проводниках поддерживаются неизменными при любых перемещениях.