Описание метода измерений

 

Тело, скатываясь с наклонной плоскости, проходит путь 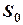и спускается с высоты . В нижней точке скорость поступательного движения максимальна и равна , где 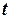– время движения от верхней точки до нижней. Угловая скорость тела в этой точке , где – радиус стержня (оси). Далее тело, проходя по инерции расстояние по наклонной плоскости, останавливается на высоте .

При движении на тело действует сила тяготения, сила реакции опоры и, не совершающая работы, сила трения покоя, приложенная в точке контакта оси с наклонной плоскостью и создающая вращающий момент относительно оси, проходящей через центр масс тела. Также на тело действует сила трения качения, которая задается величиной момента , вектор которой направлен против вектора угловой скорости. На всем пути тела до остановки момент силы трения качения совершает работу, которую можно вычислить с помощью закона сохранения механической энергии

, (1)

где – угловой путь, пройденный телом, 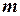– масса скатывающегося тела, = 9,81 м/с² – ускорение свободного падения.

Из уравнения (1) получаем

. (2)

Для нижней точки траектории тела запишем соотношение

(3)

и выразим из него 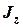– момент инерции скатывающегося тела относительно мгновенной оси вращения. При малых значениях аргумента синус можно заменить по формуле приближенных вычислений ( измеряется в радианах), тогда получаем окончательное выражение для вычисления момента инерции:

. (4)*

Здесь величина – является постоянной, которая указана на установке.

В качестве основной рабочей формулы для определения момента инерции скатывающегося тела динамическим методом выберем формулу (4), в которой масса всего тела 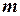, радиус оси , параметры установк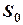и и могут быть определены с малой погрешностью. Для уменьшения влияния случайных факторов, измерения времени движения тела 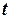и пути , проходимого телом до остановки, необходимо провести несколько раз, подставляя в выражение (4) их усредненные значения.