Дисперсионный анализ

Для определения статистической значимости показателя тесноты связи и существенности связи между результирующей и факторными переменными проводится дисперсионный анализ. Задача состоит в исследовании дисперсии результирующего показателя.

Проверка гипотезы о существенности связи результирующей и факторных переменных в уравнения регрессии (статистической значимости множественного коэффициента корреляции) осуществляется с помощью F-критерия Фишера. Величина F-критерия связана с коэффициентом детерминации R²:

.

Проверка существенности связи в уравнения регрессии с помощью F-критерия проводится при условии нормальности распределения ошибки регрессии.

Для проверки вычисляется F-статистика:

где :

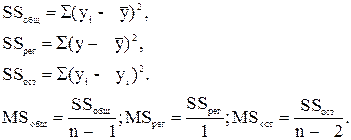
Из таблиц распределения Фишера определяется критическое значение F_df1,df2,α при заданном уровне значимости α и степенях свободы df₁ = 1, df₂ = n-2, где уровень значимости α – вероятность совершения ошибки первого рода.

Если F_pасч> F_{df1,df2,α ,} то полученное значение множественного коэффициента корреляции можно считать статистически значимым. В противном случае полагаем R = 0, что свидетельствует об отсутствии линейной зависимости между результирующей и факторными переменными в уравнения регрессии

В пакетах программ используется другой способ проверки гипотезы о существенности связи результирующей и факторных переменных в уравнения регрессии. Там автоматически рассчитывается p-уровень (p_F),т.е. значение вероятности, соответствующее расчетному значению F-критерия.

 

 

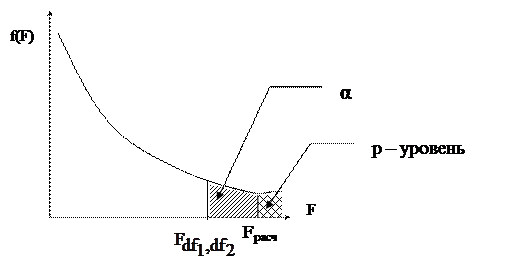
Если p_F<α, то полученное значение множественного коэффициента корреляции можно считать статистически значимым. В противном случае полагаем R = 0, что свидетельствует об отсутствии линейной зависимости между результирующей и факторными переменными в уравнения регрессии. Чем меньше значение p-уровня, тем надежнее полученные оценки.