Качение по недеформируемой поверхности.

Действуют силы P_X, P_Z, действует или отсутствует момент на колесе.

Момент М возникает в результате передачи его от полуоси н аколесо от тормозного барабана. Если момент совпадает с нарпавлением движения АТС – он считается положительным.

Реакция дороги на движущееся колесо.

Прикасаясь к дороге бесчисленым количеством точек шина образует зону контакта. В каждой точке контакта на шину действует бесконечно малая сила – это элементарная реакция дороги. Равнодействующая элементарных сил представляет собой реакцию дороги на колесо R_Z.

Реакию дороги в общем случае можно представить в виде 3-х составляющих:

- нормалной – перпендикулярно к дороге.

- касательной – действует в плоскости дороги.

- поперечной – в плоскопти дороги, но в перпендипулярном направлении.

Возникновение реакций в плоскости дророги возможно лишь при наличии нормалной реакции.

Для качения колеса к нему необходимо приложить либо силу либо момент. Если момент совпадает с направлдением вращения колеса, он называется тяговым, в противном случае – тормозным.

Разделив моменты на радиус колеса получим значение соответствующее тяговой или тормозной силы, приложеных к окружности колеса в зоне контакта.

Тяговая сила, при ее наличии направлена в сторону движения оси колеса и преодолевает силы внешних сопротивлений.

Рассмотрим взаимодействие шины с дорогой в зоне контакта.

У неподвижного колеса зона контакта шины с дорогой имеет форму близкую к элипсу и элементарные нормальные реакции расположены симметрично относительно его продольной и поперечной оси.

В силу симметричности пятна нормальная реакция R_Z будет приложена по вертикальной оси колеса.

У катящегося колеса реакция смещается на неоторое расстояние от его оси. Смещение равнодействующей R_Z обуславливается затратами энергии на преодоление трения в шине (внутренние потери).

При качении колеса деформация в передней части шины возрастате – равновесие сил нарушается, а значит происходит смещение равнодействующей. Аналогичные процессы будут протекать и для случая, когда идет движение недефлрмируемого колеса по деформируемой поверхности (будет расмотрено ниже).

Если расматривать смещение реакции дял деформируемой шины, то расстояние этого смещения из-за даформации шины обозначим а_ш, а растояние смещения по деформируемой поверхности обозначим а_д, тогда в общем случае движения колеса (движение деформируемого колеса по деформируемой поверхности) смещение определяется:

.

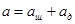В общем случае движения колеса под действием тягового момента, согласно представленых схем уавнение проекций всех сил:

- на вертикальную ось z будет иметь вид z= R_Z,

- на горизонтальную ось x : х=0.

Уравнение моментов относительно чентра колеса будет иметь вид:

.

Таким образом величина тягоового момента. Приложеного а колесу при отсутствии других сопротивлений должна компенсировать внутренние потери в шине и внешние потери – деформацию дороги. Касательная реакция дороги при этом отсутствует и момент z×a носит название момента сопротивления качению.

В случае равномерного качения колеса под действием горизонтальной силы Р_х уравнение всех сил будет иметь следующий вид:

,

- на горизонтальную ось x=-P_x;

- на вертикалдьную ось z=R_Z;

полученые формулы свидетельствуют, что касательная реакция дороги, действующая на колесо, при отсутствии н анем тягового момента равна тяговой силе. Знак "минус" указывает, что направление противоположно показаному на схеме, а значит представляет собой сопротивление движению колеса. Эта сила пропорциональна нормальной реакции:

.

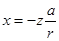Отношение 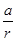называется коэфициентом сопротивления качению.

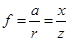, т.е. он равняется отношению наименьшей силы, вызывающей равномерное качение колеса "x" к нормальной реакции дороги "z". Произведение z×f называется силой сопротивления качению колеса .

Воздействие дороги на колесо в общем случае возможно представить силами z и x, приведенными к центру контакта, и моментом соспротивления качению. В случае равномерного качения колеса под действием момента при отсутствии других сопротивлений, касательная реакция дороги равна нулю. В случае равномерного качения колеса под действием горизонтальной толкающей силы, касательная реакция дороги представляет собой силу сопротивления качению.

Рассмотрим неравномерное качение автомобильного колеса на которое действует вертикальная и горизонтальная силы, заменяющие действие условно отброшеной массы автомобиля, тяговый момент, подведенный к полуоси ведущего колеса, а также реакция дороги и момент сопротивления качению колеса.

Вследствие неравномерности движения возникает инерционный моент, нарпавленый противоположно ускорению

,

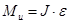где J – момент иенрции колеса и связаных с ним вращающихся деталей.

Касательная реакция дороги, действующая на ведущее колесо:

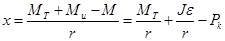(1)

В случае , если к колесу не приложен тяговый момкент М_Т, то касательная реакция будет предвтсалена, как:

.

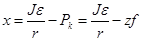Знак "минус" указыват на то, что реакция в данном случае напрпавлена противоположно движению колеса.

Согласно выражению (1) касательная реакция на ведущем колесе увеличивается при увеличинии тягового момента, однако это увеличесние не может быть сколько угодно большим. Максимальное значение касательной реакции ограничено сцеплением шины с дорогой. Предельная величина касательной реакции по сцеплению называется силой сцепления шины с дорогой. Эта величина пропорциональна нормальной реакции дороги:

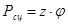, где j - коэфициент сцепления.

Коэфициент сцепления числено равен отношению ниаменьшей силы, вызывающей равномерное скольжение колеса к нормальной реакции дороги. В зависимости от направления скольжения различают коэфициенты продоллльного j_х и поперечного j_y сцепления. Отождествление коэфициентов сцепления с коэфициентом трения скольжения не совсем верно, т.к. при сцеплении колес и дороги наблюдается на только трение, но и механическое зацепление поверхностей.

Существует параметр, определяющий динамику автомобилного колеса. Это т.н. окрыжная сила колеса, представляющая собой отношение момента, приложеного к колесу к радиусу качения:

.

Этот показатель явялется обобщенной силой на каком-то пути S, проходимом колесом автомобиля. Коэфициенты количественно характеризующие сопротивление качеению колеса, т.е. коэфициент сопротивления качению f, представляющий собой сумму составляющих f_c и f_r являются соответственно энергетическим, силовым и кинематическим коэфициентами сопротивления качению, а полная окружная сила явялтеся колмичсественой характеристикой нагружения колеса. Она равна продольной силе, действующей со стороны колеса на автмобиль при отсутствии энергетических потрерь на качение и измененти его кинематической энергии во вращательном дфижении.

Отношение 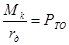является полной тяговой силой, она равна продольной силе, действующей со стороны колеса на автмобиль при отсутствии силовых потерь на качение колеса и изменение его кмнетической энергии во вращательном движении. Исходя из схемы сил и моментов, прилагаемых к движущемуся колесу, возможно составить т.н. силовой баланс колеса.

(2)

Равенство характеризует силовой баланс и его сид может изменяться в зависимости от режима качения колеса, определяемого значениями и направлениями момента М и реакции R_x.