Понятие о стохастическом программировании (СТП)

В задаче линейного программирования

;

( );

( )

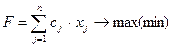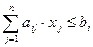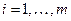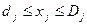величины , , 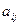, , 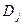заданы. Часто на практике величины , , 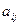могут быть случайными. Так, если - ресурс, то он зависит от ряда факторов. Аналогично, цены будут зависеть от спроса и предложения, расходные коэффициенты 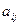- от уровня техники и технологии.

Задачи, в которых , , 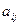- случайные величины, относят к задачам стохастического программирования.

В задачах стохастического программирования случайный характер величин указывают двумя способами:

1) реализацией случайных величин;

2) законом распределения случайных величин.

В первом случае в модель подставляют фактические значения случайных величин и решают задачу для этих значений. Получается обычная ЗЛП.

Недостатки:

- необходимость иметь значения реализации случайных величин, что не всегда возможно;

- невозможно составить план, т.к. в момент составления плана на предстоящий период конкретных значение реализации случайных величин в принципе быть не может.

Во втором случае по закону распределения случайных величин эти недостатки отсутствуют. Обычно принимают, что случайные величины подчиняются нормальному закону распределения, заданному математическим ожиданием и дисперсией.

Задача стохастического программирования предусматривает стохастическую постановку целевой функции и ограничений.

Стохастическая постановка целевой функции может быть двух видов: М-постановка и Р-постановка.

При М-постановке случайная величина заменяется ее математическим ожиданием и задача сводится к оптимизации детерминированной целевой функции:

;

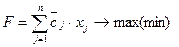где - математическое ожидание случайной величины .

При Р-постановке целевая функция будет иметь вид:

- при максимизации целевой функции

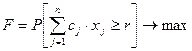
означает максимизацию вероятности того, что случайная величина 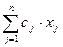будет не меньше некоторого значения r;

- при минимизации целевой функции

означает минимизацию вероятности того, что случайная величина 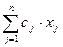будет не больше некоторого значения r.

Для ограничений задачи стохастического программирования наиболее распространены стохастические постановки в вероятностных ограничениях вида:

(1)-(2)

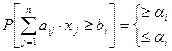(3)-(4)

где 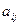, - случайные величины, 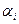- заданные уровни вероятности. Так, ограничение (1) означает, что вероятность соблюдения неравенства 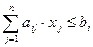должна быть не меньше, чем 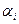. Аналогичный смысл и др ограничений.

Для случая, когда вероятностные ограничения представлены в виде типа (1), задачу СТП можно записать в виде:

- при М-постановке

;

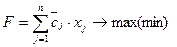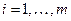( ); (5)

( )

 

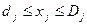- при Р-постановке

- в случае максимизации целевой функции

;

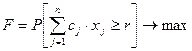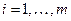( ); (6)

( )

 

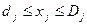- в случае минимизации целевой функции

;

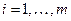( ); (7)

( )

 

где , , 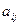- случайные величины.

Для случаев ограничений (2)-(4) постановка задач СТП аналогична.

Задачи (5)-(7) непосредственно решены быть не могут. Одним из возможных методов их решения может быть представление их в виде детерминированного эквивалента.