Москва 2011

Составители доценты Новикова Т. П. и Соболь Л. В.

УДК 519.2 (076.5)

Математическая статистика: Методическое указание по изучению дисциплины/ Рос. гос. агр. заоч. ун-т./ Составители Т. П. Новикова и Л. В. Соболь, М., 2011-11-07 Предназначены для студентов 1*, 2 курсов.

Утверждены методической комиссией факультета механизации и технического сервиса ФГОУ ВПО РГАЗУ.

Рецензенты: д.т.н. профессор В. И. Славкин, д.т.н. профессор А. А. Симдянкин (ФГОУ ВПО РГАЗУ)

Раздел 1. ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ

Дисциплина «Теория вероятностей и математическая статистика» отно­сится к базовой (обязательной) части второго цикла ООП. Методические указа­ния по данной дисциплине составлены в соответствии с требованиями Феде­рального государственного образовательного стандарта высшего профессио­нального образования (ФГОС ВПО) третьего поколения по направлению «Агрономия», утвержденного приказом Министерства образования и науки Российской Федерации 22 декабря 2009 г. Ха 811, примерной программой по дисциплине и рабочими учебными планами, утвержденными ученым советом ФГОУ ВПО РГАЗУ 26 января 2011 г.

1.1.Цели и задачи дисциплины

Цель дисциплины - развитие навыков математического мышления; навы­ков использования математических методов и основ математического модели­рования; математической культуры у обучающегося.

Ему необходимо в достаточной степени владеть как классическими, так и современными математическими методами анализа задач, возникающих в его практической деятельности, использовать возможности вычислительной техни­ки, уметь выбирать наиболее подходящие комбинации известных методов, знать их сравнительные характеристики.

Для выработки у современных специалистов с высшим образованием не­обходимой математической культуры необходимо решение следующих задач:

1.Обеспечение высокого уровня фундаментальной математической под­готовки студентов.

2.Выработка у студентов умения проводить логический и качественный анализ социально-экономических задач управления на основе построения ма­тематических моделей на базе различных средств информационного обеспечения.

3.Умение использовать методы современной математики, необходимые для работы по выбранной специальности.

4.Умение специалиста самостоятельно продолжить свое математическое образование.

В результате изучения дисциплины студент должен:

1)обладать следующими общекультурными компетенциями (OK):

- владением культурой мышления, способностью к обобщению, анализу, вос­приятию информации, постановке цели и выбору путей ее достижения (ОК-1);

- умением логически верно, аргументировано и ясно строить устную и пись­менную речь (ОК-2);

2)обладать следующими профессиональными компетенциями (ПК):

- способностью к использованию основных законов естественнонаучных дис­циплин в профессиональной деятельности, применением методов математиче­ского анализа и моделирования (ПК-1);

- способностью проводить и оценивать результаты измерений (ПК-5);

- готовностью к обработке результатов экспериментальных исследований.

В результате изучения дисциплины студент должен:

- знать: методы теории вероятностей и математической статистики;

- уметь: использовать аппарат теории вероятностей и математической статистики при изучении количественных закономерностей, которым подчи­няются массовые случайные события;

- владеть: навыками решения задач по теории вероятностей и математи­ческой статистики.

1.2. Библиографический список

Основной

1. Гмурман В.Е. Теория вероятностей и математическая статистика. М.:
Высшая школа, 2002.

2.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 2002.

3.Кудрявцев В.А., Демидович В.П. Краткий курс высшей математики. М.: Наука, любое издание.

Дополнительный

4.Лычкин В. Н. Высшая математика в задачах: Учебное пособие. М.: Изд-во ФГОУ ВПО РГАЗУ, 2009.

5.Лычкин В. Н. Высшая математика: Учебное пособие. М.: Из-во ФГОУ ВПО РГАЗУ, 2011

 

1.3 Распределение учебного времени по модулям (разделам) и темам дисциплины

 

	В том числе, ч
Наименование модулей и тем дисциплины	Всего, ч	лекции	Практические занятия	Самостоятельная работа	Рекомендуемая литература
Модуль 1. Основные понятия математической статистики		2 (2)	2 (2)	31 (31)	1-5
Модуль 2. Статистические оценки параметров распределения		2 (2)	2 (2)	26 (26)	1-5
Модуль 3. Элементы теории корреляции		2 (-)	2 (-)	26 (30)	1-5
Модуль 4. Проверка статистических гипотез		- (-)	2 (-)	23 (13)	1-5
Модуль 5. Дисперсионный анализ		- (-)	- (-)	24 (-)	1-5
Итого		6 (4)	8 (4)	130 (100)

 

Примечание: в скобках указаны часы для студентов с сокращенным сроком обучения.

 

 

Раздел 2. СОДЕРЖАНИЕ УЧЕБНЫХ МОДУЛЕЙ ДИСЦИПЛИНЫ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИХ ИЗУЧЕНИЮ

2.1. Модуль 1. Основные понятия математической статистики

2.1.1. Содержание модуля

Генеральная совокупность и выборка. Вариационный ряд. Гистограмма, эмпирическая функция распределения, выборочная средняя и дисперсия.

2.1.2 Методические указания по его изучению.

После изучения по учебникам теоретического материала разберите решение примера номер 1.

Пример 1.По некоторому региону известна ежедневная прибыль (в тысячах рублей) двадцати однотипных торговых предприятий: 11,3; 10,2; 13,9;

10,7; 11,8; 8,2; 12,4; 9,6; 13,1; 10,6; 6,3; 11,3; 10,2; 15,1; 10,5; 11,0; 15,1;

11,6; 10,4; 11,7. Составить интервальный ряд распределения и начертить гистограмму распределения плотности относительных частот.

Решение. Запишем исходные данные в виде ранжированного ряда:

6,3; 8,2; 9,6; 10,2; 10,2; 10,4; 10,5; 10,6; 10,7; 11,0; 11,3; 11,3; 11,6; 11,7;

11,8; 12,4; 13,1; 13,9; 15,1; 15,1. Из этого ряда видно, что диапазон изменения вариант выборке составляет 6 – 16. Этот диапазон разобьем на несколько интервалов. Размер интервала выбирается произвольно, но следует иметь в виду, что чем меньше интервал, тем точнее результаты. В нашем случае принимаем размер интервала равным 2 единицам, то есть 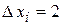. Получаем пять интервалов: первый 6 – 8, второй 8 – 10, третий 10 – 12, четвертый 12 – 14, пятый

14 – 16.

Определяем частоту попадания вариант выборки в каждый интервал.

В первый интервал попадает одно значение ряда – 6,3 , поэтому . Во второй интервал попадают два значения – 8,2 и 9,6 , поэтому . Аналогично находим , , .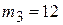

Определяем относительные частоты попадания вариант выборки в каждый интервал:

в первый интервал - ;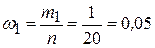

во второй интервал - ;

в третий интервал - ;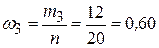

в четвертый интервал - ;

в пятый интервал - .

Сумма , следовательно , вычисления выполнены верно.

Определим плотность относительных частот вариант как отношение относительной частоты к длине интервала :

для первого интервала - ;

для второго интервала - ;

 

для третьего интервала - ;

для четвертого интервала - ;

для пятого интервала - .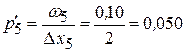

Результаты выполненных расчетов сводим в таблицу.

 

Таблица

Интервальный ряд распределения прибыли предприятий

Интервал значений прибыли	6 - 8	8 – 10	10 - 12	12 - 14	14 - 16
Частоты вариант
Относительные частоты	0,05	0,10	0,60	0,15	0,10
Плотность относительных частот	0,025	0,050	0,300	0,075	0,050

 

 

Построим гистограмму, показывающую зависимость плотности относительных частот от значения вариант. По горизонтальной оси наносим шкалу возможных значений вариант, по вертикальной оси – плотность относительных частот; величину относительной плотности считаем постоянной внутри соответствующего интервала. Получаем столбчатую диаграмму (рис.1), называемую гистограммой распределения плотности относительных частот.

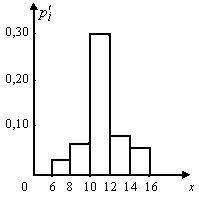
Рис. 1

 

2.1.3. Вопрос для самоконтроля

1. Что понимается под генеральной совокупностью?

2. Что такое выборка вопроса? Как обеспечивается её представительность?

3. Что такое частота появления варианты выборки?

4. Как получают относительную частоту варианты в выборке?

5. Как получают вариационный ряд распределения?

6. Как строится многоугольник распределения относительных частот?

7. Как построить гистограмму распределения плотности относительных частот?

 

2.1.4. Задания для самостоятельной работы.

1. Составить вариационный ряд и построить многоугольник распределения относительных частот по следующей выборке:

1; 1; 2; 3; 3; 6; 5; 3; 1; 8; 2; 5; 5; 2; 2; 8; 3; 1; 1; 1.

Диапазон значений случайной величины разбить на 5 интервалов.

 

 

2.2. Модуль 2. Статистические оценки параметров распределения.

2.2.1. Содержание модуля

Статистические оценки генеральной средней и доли. Погрешность оценки. Доверительная вероятность и доверительный интервал. Определение дополнительного объема выборки.

2.2.2. Методические указания по его изучению.

После изучения по учебникам теоретического материала разберите решение примеров 2 и 3.

Пример 2.Дана выборка значений нормально распределенного признака Х ( в первой строке указаны значения признака , во второй - соответствующие им частоты ):

20 30 40 50 60 70 80

4 11 25 30 15 10 5

Найти : 1) выборочную среднюю 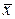и исправленное среднее квадратичное отклонение s методом произведений; 2) доверительный интервал, покрывающий с надежностью 0,95 неизвестное математическое ожидание а признака Х; 3) доверительный интервал, покрывающий неизвестное среднее квадратическое отклонение признака Х ( надежность оценки во всех вариантах считать равной = 0.95 ).

Решение. 1) Для нахождения выборочной средней 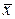и выборочной дисперсии D_в составим расчетную таблицу, для чего: а) запишем варианты

в первый столбец, частоты - во второй столбец; б) в качестве «ложного нуля» С берем варианту 50 (она имеет наибольшую частоту); в клетке третьего столбца, которая принадлежит строке, содержащей варианту 50, пишем 0; под нулем последовательно записываем условные варианты - 1, - 2, - 3, а под нулем – последовательно 1, 2, 3; в) в четвертый столбец записываем произведения ; отдельно находим сумму (- 59) отрицательных и отдельно сумму (50) положительных чисел; сложив эти числа, их сумму (- 9) записываем в нижнюю клетку столбца; г) в пятый столбец записываем произведения , в шестой – произведения ; в нижней строке каждого из этих столбцов записываем сумму чисел этого столбца.

В итоге получаем следующую расчетную таблицу:

 

 

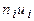
		- 3 - 2 - 1	- 12 - 22 - 25 - 59
	n = 100		∑ = - 9	∑ = 205	∑ = 287

Контроль:

∑ + 2 ∑ + n =205 – 18 + 100 = 287.

∑ = 287.

Совпадение найденных сумм свидетельствует о том, что вычисления произведены правильно.

Вычислим условные моменты первого и второго порядков:

; .

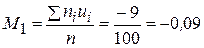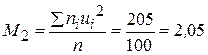Находим шаг h (разность между двумя соседними вариантами):

h = 30 – 20 = 10.

Находим выборочную среднюю:

.

Находим выборочную дисперсию:

.

Находим исправленную дисперсию:

.

Исправленное среднее квадратическое отклонение равно

.

2). Искомый доверительный интервал для математического ожидания а имеет вид 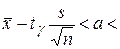, где 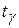находим из таблицы 3

Приложений. При γ = 0,95 и n = 100 получаем 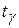= 1,984. Тогда

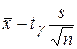= 49,1 – = 46,25.

= 49,1 + = 51,95.

Таким образом,

46,25 < a < 51,95.

3). Доверительный интервал для генерального среднего квадратического отклонения σ имеет вид

, если q < 1 и

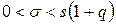, если q ≥ 1,

где соответствующие значения q находятся в таблице 2 приложений.

По заданным γ = 0,95 и n = 100 находим q = 0,143. Тогда искомый доверительный интервал есть

14,36(1− 0,143) < σ < 14,36(1+ 0,143) или 12,31 < σ < 16,41.

Пример 3.Для определения средней урожайности сахарной свеклы в хозяйстве на площади 1000 га была определена ее урожайность на 100 га. Результаты выборочного обследования представлены следующим распределением:

 

Урожайность, ц / га	23-25	25-27	27-29	29-31	31-33	33-35	35-37
Площадь, га

 

Найти: 1) величину, которую можно принять за среднюю урожайность на всем массиве; 2) величину, которую следует принять за среднее квадратическое отклонение урожайности на всем массиве; 3) доверительный интервал, в котором с вероятностью 0,95 заключена средняя урожайность на всем массиве.

Решение. 1) В качестве приближенного значения средней урожайности на всем массиве принимаем среднюю арифметическую данного в условии распределения, то есть выборочную среднюю:

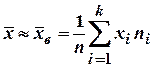. Здесь .

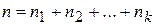За значение признака нужно принять середины интервалов.

Получим:

.

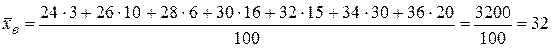Значит, приближенное значение средней урожайности на всем массиве будет х≈32 ц.

2) Для оценки дисперсии генеральной совокупности применяем формулу

; .

 

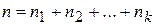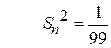[3(24 – 32)² + 10(26 – 32)² + 6(28 – 32)² + 16(30 – 32)² +

+ 15(32 – 32)² + 30(34 – 32)² + 20(36 – 32)² ] =

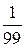= (192 + 360 + 96 + 64 + 0 + 120 + 320) = 1152 = 11,64.

Значит, приближенное значение дисперсии на всем массиве будет , отсюда среднее квадратическое отклонение урожайности на всем массиве равно

.

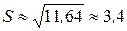Найдем среднее квадратическое отклонение выборочной средней по формуле

.

Получаем ц.

Итак, оценка средней урожайности сахарной свеклы на всем массиве равна 32 ц. со средней квадратической ошибкой 0,34 ц. Оценка среднего квадратического отклонения урожайности на всем массиве равна 3,4 ц.

3) Для вычисления доверительного интервала воспользуемся равенством

,

согласно которому можно утверждать, что с надежностью γ доверительный интервал покрывает неизвестное математическое ожидание, точность оценки .

Поскольку n = 100 > 30, пользуемся нормальным распределением. Значит,

.

Из равенства следует и по таблице 1 приложений находим . Следовательно, точность оценки

.

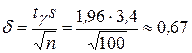Концы доверительного интервала и

.

Таким образом, с вероятностью 0,95 средняя урожайность сахарной свеклы на всем массиве заключена в границах от 31,33 ц до 32,67 ц.

 

2.2.3. Вопросы для самоконтроля.

1. Как вычисляется средняя арифметическая выборки при малом и больших её объемах?

2. Как вычисляется дисперсия выборки в случаях малого и большого её объемов?

3. Какая величина принимается за среднюю генеральной совокупности, а какая – за дисперсию?

4. Что понимается под доверительным интервалом и доверительной вероятностью?

5. Как вычисляется среднее квадратическое отклонение средней выборки?

6. Какова вероятность попадания генеральной средней в интервал размером ±2(±3) средних квадратических отклонений средней выборки при нормальном распределении?

2.2.4. Задания для самостоятельной работы.

1. Даны выборочные варианты хi и соответствующие им частоты ni нормально распределенного признака X:

хi 20 30 40 50 60 70 80

ni 4 11 25 30 15 10 5

Найти. 1) выборочную среднюю х иисправленное среднее квадратическое отклонение s методом произведений; 2) доверительный интервал, покрывающий с надежностью 0,95 неизвестное математическое ожидание a признака Х; 3) доверительный интервал покрывающий с надежностью 0,95 неизвестное среднее квадратическое отклонение ϭ признака Х.

 

2.3. Модуль 3. Элементы теории корреляции.

2.3.1. Содержание модуля.

Функциональная зависимость и регрессия. Кривые регрессии, их свойства. Коэффициент корреляции, корреляционное отношение, их свойства и оценки. Определение параметров линейной регрессии методом наименьших квадратов. Определение параметров нелинейных уравнений регрессии методом наименьших квадратов непосредственно и с помощью линеаризующих замен переменных. Оценка параметров многомерных линейных функций регрессии. Совокупный и частный коэффициенты множественной корреляции, свойства и оценки.

 

2.3.2. Методические указания по его изучению.

После изучения по учебникам теоретического материала разберите решение примера 4.

Пример 4.Были проведены измерения общей длины ствола в см ( Х) и длины его части без ветвей (У) десяти молодых сосен. Результаты этого измерения представлены в следующей таблице

 

Х
У

 

Вычислить выборочный коэффициент корреляции и найти выборочное уравнение прямой регрессии У на Х.

Решение. Выборочный коэффициент корреляции вычислим по формуле

 

.

Для вычисления величин, входящих в эту формулу, составим вспомогательную таблицу, в которой результаты измерений записаны столбцами. Внизу каждого из этих столбцов вычислены суммы для нахождения средних и . Далее расположены столбцы, в которых вычисляются разности и , их квадраты и произведения. Значения этих суммируются, чтобы получить величины, необходимые для подстановки в формулу. Отметим, что суммы в столбцах, в которых вычислены разности

и будут всегда равны нулю.

 

						( )( )
		- 45 - 35 - 25 -15 - 5		- 9 - 5 - 4 - 3

Находим средние и :

= ; = .

Из таблицы имеем

( )( ) = 1520, = 8250 , = 298.

Подставляя эти значения в формулу для вычисления коэффициента корреляции, получим

.

Таким образом, у выбранных сосен имеет место очень сильная корреляция между общей длиной ствола и длиной его части без ветвей.

Далее найдем выборочное уравнение прямой регрессии У на Х. Это уравнение имеет вид .

За приближенные значения и принимают соответственно

; .

Тогда

.

Подставляя в выборочное уравнение прямой регрессии У на Х

, получим

или .

Окончательно, - искомое уравнение прямой регрессии У на Х.

2.3.3. Вопросы для самоконтроля.

1. Дайте определение корреляционной зависимости.

2. Какая корреляционная зависимость называется линейной?

3. Дайте определение выборочного коэффициента корреляции и перечислите его свойства.

4. Запишите выборочные уравнения прямых регрессий.

5. В чем суть метода наименьших квадратов для определения параметров линии регрессии?

6. В каком случае корреляцию называют криволинейной?

 

2.3.4. Задания для самостоятельной работы.

1. Вычислить выборочный коэффициент корреляции и найти выборочное уравнение прямой регрессии У на Х. Данные взять из следующей таблицы

х
у

 

2. Вычислить выборочный коэффициент корреляции двух случайных величин х и у и найти выборочное уравнение прямой регрессии У на Х.

Данные взять из таблицы.

х
у

 

 

2. 4. Модуль 4. Проверка статистических гипотез.

2.4.1. Содержание модуля.

Принцип проверки статистической гипотезы. Методика статистической проверки гипотез о средних дисперсиях, о нормальном распределении генеральной совокупности.

2.4.2. Методические указания по его изучению.

После изучения по учебникам теоретического материала разберите решение примера 5.

Пример 5. Используя критерии Пирсона, при уровне значимости 0,05 установить, случайно или значимо расхождение между эмпирическими частотами ni и теоретическими частотами ni´, которые вычислены исходя из гипотезы о нормальном распределении генеральной совокупности Х:

ni
n´i

 

Решение. Для того, чтобы при заданном уровне значимости a проверить нулевую гипотезу Н0: генеральная совокупность распределена нормально, надо:

а) вычислить наблюдаемое значение критерия

=Ʃ ;

б) по таблице критических точек распределение χ² , по заданному уровню значимости α и числу степеней свободы k=s-3 (s–число групп выборки), найти критическую точку ˂ – нет оснований отвергнуть нулевую гипотезу. Другими словами, эмпирические и теоретические частоты различаются незначимо (случайно). Если ˃ – нулевую гипотезу отвергают. Другими словами, эмпирические и теоретические частоты различаются значимо. Воспользуемся этим правилом. Вычислим

= + + ≈1,52

Учитывая, что число групп выборки (число различных вариант) s=9, найдём число степеней свободы

K=s-3=9-3=6

По таблице критических точек распределения χ² (таблица 3 приложение), по уровню значимости α=0,05 и числу степеней свободы k=6, находим критическую точку (0,05;6)=12,6. Так как ˂ - нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

2.4.3. Вопросы для самоконтроля

1. Дайте определение статистической гипотезы.

2. Приведите примеры нулевой и конкурирующей, простой и сложной гипотез.

3. Что называют ошибкой первого (второго) рода?

4. Что такое уровень значимости? Приведите значение уровней значимости, наиболее употребительных на практике.

5. Дайте определение критической области, области принятия гипотезы и критических точек.

6. Как находят критическую область? В чем состоит основной принцип проверки статистической гипотезы?

7. Что называют распределением Фишера-Снедекора?

8. Как сравнивают дисперсии нормальных генеральных совокупностей?

 

2.4.4. Задания для самостоятельной работы.

1. Даны исправленные выборочные дисперсии = 0,72 и =0,20, найденные по двум независимым выборкам объемов =13 и = 18, извлеченным из нормальных генеральных совокупностей X и Y . Требуется при заданном уровне значимости α=0,01 проверить нулевую гипотезу : D(X)> D(Y) о равенстве генеральных дисперсий при указанной конкурирующей гипотезе .

2. Требуется при уровне значимости α= 0,05 проверить по критерию согласия Пирсона гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические частоты и теоретические частоты

 

 

2.5. Модуль 5. Дисперсионный анализ.

2.5.1. Содержание модуля.

Сущность дисперсионного анализа. Дисперсия комплекса. Общая, факторная и остаточная дисперсия. Приведение дисперсий к одной степени свободы. Однофакторный комплекс. Практические приемы расчета однофакторного комплекса при оценке результатов полевых испытаний.

2.5.2. Методические указания по его изучению.

После изучения по учебникам теоретического материала разберите решение примера 6.

Пример 6. Опыты по определению влияния доз удобрений на урожайность некоторой культуры дали следующие результаты:

Номер наблюдения	Урожайность при различных дозах удобрения
I	II	III

Методом дисперсионного анализа при уровне значимости 0,05 проверить нулевую гипотезу о равенстве групповых средних, то есть определить, существенны ли различия между средними.

Решение. Вычислим среднюю общую и факторные (групповые):

= =71

= =73

= =60

= =80

Вычислим суммы квадратов отклонений:

=Σ( - )²=(70-71)²+(80-71)²+(64-71)²+(78-71)²+(86-71)²+(70-71)²+(79-71)²+(85-71)²+(46-71)²+(68-71)²+(55-71)²+(71-71)²=1556

=q =4 =824

= =1556-824=732

Находим дисперсии факторную и остаточную

= = =41;

= = =81,3.

Здесь p-число постоянных уровней фактора: р=3, q- число испытаний на каждом уровне: q=4.

Сравним факторную и остаточную дисперсии по критерию Фишера-Снедекора. Для этого сначала найдем наблюдаемое значение критерия:

= = =5,07.

Учитывая, что степеней свободы числителя а знаменателя =p(q-1)=3(4-1)=9 и что уровень значимости α=0,05, по таблице 4 приложения находим критическую точку

=(0,05;2;9)=4,26

Так как ˃ , то нулевую гипотезу о равенстве групповых средних отвергаем. Следовательно, средние различаются между собой существенно, влияние доз удобрений на урожайность культуры значимо.

 

2.5.3 Вопросы для самоконтроля.

1. В чем суть дисперсионного анализа?

2. Приведите классификацию моделей дисперсионного анализа в зависимости от числа факторов и от цели исследования.

3. Какая вероятностная модель лежит в основе однофакторного дисперсионного анализа?

4. Как вычисляются общая, факторная и остаточная суммы квадратов отклонений?

5. Как связаны между собой общая, факторная и остаточная суммы квадратов отклонений?

6. Как вычисляются общая, факторная и остаточная дисперсия?

7. Как сравнивают несколько средних методом дисперсионного анализа?

2.5.4. Задания для самостоятельной работы.

1. Приведены результаты четырех испытаний на каждом из трех уровней фактора F. Методом дисперсионного анализа при уровне значимости 0,05 проверить нулевую гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных генеральных совокупностей с одинаковыми дисперсиями.

Номер испытания	Уровни фактора