Лабораторна робота №1

 

ПОБУДОВА ОДНОМІРНИХ РЯДІВ
ЗА РЕЗУЛЬТАТАМИ ВИМІРЮВАНЬ

 

Мета: навчитись будувати ранжируваний та варіаційний ряди,
вираховувати основні статистичні характеристики:

Мо – моду;

Ме – медіану;

– середнє арифметичне значення;

σ² – дисперсію;

σ – середнє квадратичне відхилення;

V – коефіцієнт варіації;

– помилку середнього арифметичного.

 

ТЕОРЕТИЧНІ ВІДОМОСТІ

Статистичні методи обробки результатів вимірів

Предметом математичної статистики є аналіз результатів масових, повторюваних вимірів. Результати таких вимірів завжди більш-менш відрізняються один від одного. Навіть якщо виміряється той же самий об'єкт у незмінних умовах, не можна одержати однакових даних. Через численні причини, що не піддаються контролю і варіюють від одного виміру до іншого, результати вимірів завжди мають випадкове розсіювання. Аналогічне розсіювання буває при однотипних вимірах у групі однорідних об'єктів (вимірювання висоти стрибка в школярів одного класу). Хоча результат кожного окремого виміру при випадковому розсіюванні заздалегідь передбачити не можна, це не означає, що ми маємо справу з повним хаосом. Масові виміри однорідних об'єктів, що володіють якісною спільністю, виявляють певні закономірності. Математична статистика створює методи виявлення цих закономірностей. Виділяють три основних етапи статистичних досліджень.

I. Статистичне спостереження, що являє собою планомірний, науково обґрунтований збір даних, які характеризують досліджуваний об'єкт. Воно повинне задовольняти наступним вимогам:

а) об'єкти спостереження (в окремому випадку випробувані) повинні бути однаковими (однорідними) з погляду їхніх властивостей (кваліфікація, спеціалізація, вік, стаж занять тощо);

б) число об'єктів спостереження повинне бути достатнім, щоб
можна було виявити закономірності й узагальнити їх властивості.

ІІ. Статистичне зведення і групування. Вони є важливою підготовчою частиною до статистичного аналізу даних. Цей етап передбачає:

а) систематизацію (групування) даних;

б) оформлення певних статистичних таблиць.

III. Аналіз статистичного матеріалу. Це завершальний етап статистичного підходу. Його здійснюють з використанням відповідних математико-статистичних методів.

 

Одномірні ряди результатів вимірів. Складання рядів розподілу

У процесі спостереження чи виміру будь-якого показника одержують ряд чисел. Чисельні результати поділяють на дискретні (від англ. discrete – перериваний) і безупинні. До дискретних належать число підтягувань на поперечині, число спроб тощо, тобто результати, що виражаються цілим числом; до безупинних – час проходження дистанції, час реакції, швидкість руху тощо, тобто результати, що можуть виражатися дробовим числом, зокрема нескінченним дробом.

Будемо вважати, що х₁ – результат виміру досліджуваного показника в 1-го спортсмена, х₂ – у 2-го спортсмена тощо. Усього спортсменів – n. Такий ряд результатів вимірів, представлений випадковими числами, називається вибіркою чи вибірковою сукупністю.

Сукупність усіх значень, які можна було б одержати для досліджуваної вибірки, називається генеральною сукупністю. Наприклад, довжина тіла студентів одного інституту фізичної культури – вибіркова сукупність, а довжина тіла студентів усіх інститутів фізичної культури – генеральна; у той же час довжина тіла студентів – вибірка стосовно генеральної сукупності – усіх студентів земної кулі.

Генеральну сукупність умовно можна представити так: це всі об'єкти спостереження (спортсмени, наприклад), які мають ті ж властивості, що й об'єкти вибірки. Однією з основних характеристик вибірки є її об’єм – n, що визначається числом об'єктів спостереження (наприклад спортсменів) у даному дослідженні.

Як здійснюється упорядкування й аналіз вибірки?

Ранжируванням називають розміщення результатів вимірів у порядку збільшення чи зменшення.

 

Вибірки великого обсягу розбивають на інтервали. У найпростішому випадку їх може бути два. Наприклад, коли необхідно відібрати гірших і кращих спортсменів. Однак для одержання досить точних результатів число інтервалів (його позначають буквою k) повинне бути більше.

Варіанта – числа, які являють собою результати вибірки.

Частота – повторюваність значень вибірки в кожному інтервалі. Вона визначається числом результатів вимірів, які попали в даний інтервал. Сума всіх частот інтервалів завжди дорівнює об’єму вибірки.

Частість – відносна частота, тобто відношення частоти до загального числа спостережень (може виражатися у %).

Накопичена частість – число варіант із значенням меншим або яке дорівнює даній варіанті.

 

 

ХІД РОБОТИ

1. Заносимо показники вимірювань (наприклад, значення вагових показників певної групи досліджуваних):

 

х₁ = 70; х₁₁ = 72; х₂₁ = 84;

х₂ = 74; х₁₂ = 61; х₂₂ = 77;

х₃ = 87; х₁₃ = 77; х₂₃ = 74;

х₄ = 77; х₁₄ = 90; х₂₄ = 66;

х₅ = 82; х₁₅ = 69; х₂₅ = 82;

х₆ = 84; х₁₆ = 80; х₂₆ = 78;

х₇ = 63; х₁₇ = 78; х₂₇ = 82;

х₈ = 78; х₁₈ = 72; х₂₈ = 77;

х₉ = 77; х₁₉ = 70; х₂₉ = 70;

х₁₀ = 69; х₂₀ = 68; х₃₀ = 75.

 

2. Виконуємо ранжирування і будуємо таблицю 1.

 

Ранжирувані значення показника (ранжируваний ряд): __________________________________________________________

 

 

Таблиця 1

№ інтервалу	Межі інтервалу	Частота	Накопичена частота	Частість, %	Накопичена частість

 

3. Будуємо графік розподілу значень показника.

 

 

Рис.1. Гістограма розподілу

 

Робимо висновки за графіком про однорідність вибірки за завданим показником, враховуючи наступні моменти:

– якщо гістограма за своїм виглядом наближується до графіка нормального розподілу величин, то група, можливо, однорідна;

– якщо графіки низькі та розтягнуті, то група, можливо, однорідна, але не компактна;

– якщо графіки мають 2 та більше вершин, то група неоднорідна за даною ознакою, її необхідно поділити на підгрупи, щоб з кожною з підгруп проводити заняття за індивідуальним планом.

 

4. Знаходимо моду (М_о) і медіану (Ме).

 

Мода – результат вибірки чи сукупності, який найбільш часто зустрічається в цій вибірці (М_о – ).

 

Медіана – результат вимірювання, який знаходиться в середині ранжируваного ряду (М_е – ).

 

5. Будуємо таблицю 2.

Таблиця 2

№ з/п	х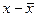
… ∑

 

5. Вираховуємо основні статистичні показники:

– середнє арифметичне:

;

 

σ² – дисперсію (вказує на розсіювання варіантів біля середнього арифметичного):

;

 

σ – середнє квадратичне відхилення (вказує на розсіювання варіантів біля середнього арифметичного у квадраті). Для σ≤30, n-1.

;

 

V – коефіцієнт варіації (показує, яку частину складає середнє квадратичне відхилення – фактор розсіювання – від середнього арифметичного); у спортивній практиці коливання результатів вимірювань в залежності від величини коефіцієнта варіації вважають невеликою (0-10 %), середньою (11-20 %) та великою (V>20%):

return false">ссылка скрыта

 

;

– помилка середнього арифметичного:

 

6. Висновок.

Література

1. Иванов В.С. Основы математической статистики. – М.: ФиС, 1990. – С. 22-30.

2. Начинская С.В. Основы математической статистики. – К.: Вища школа, 1987. – 190 с.

3. Спортивная метрология /Под ред. В.М.Зациорского. – М.: ФиС, 1982. – С. 18-31.

Лабораторна робота № 2

 

ВИЗНАЧЕННЯ КОРЕЛЯЦІЙНОГО ВЗАЄМОЗВ’ЯЗКУ
МІЖ ДОСЛІДЖУВАНИМИ ПОКАЗНИКАМИ

 

Мета:навчитись визначати наявність, форму та ступінь взаємозв’язку між показниками при лінійній залежності.

 

 

ТЕОРЕТИЧНІ ВІДОМОСТІ

1. Функціональна й кореляційна залежності

У природі багато явищ і процесів взаємопов’язані між собою. У фізичній культурі й спорті, у спортивній команді та в організмі спортсмена теж існує багато взаємозв'язків між різними показниками. Наприклад, з підвищенням кількості людей, які займаються в будь-якому виді спорту підвищуються результати в цьому виді; ускладнення у взаєминах між гравцями однієї команди погіршує її результативність; з підвищенням інтенсивності навантаження у спортсмена підвищується пульс, збільшується швидкість кровотоку в працюючих м'язах, зменшуються в них енергетичні ресурси; регулярність тренувань, оптимально підібрані навантаження за їх видом, об'ємом й інтенсивністю поліпшують результати спортсмена тощо.

Вплив одних показників на інші може бути позитивним і негативним. Фахівець повинен добре розбиратися в таких взаємозв'язках у своїй галузі, усувати або зменшувати негативний вплив і вміти вчасно та в достатній мірі використовувати корисні взаємозв'язки.

Деякі методи математичної статистики можуть допомогти будь-якому фахівцеві виявити взаємозв'язки, розкрити їх особливості. Одним з таких методів є метод кореляційного аналізу. Він спрямований на те, щоб на основі статистичного матеріалу виявити факт впливу однієї ознаки на іншу, установити користь або шкоду цього впливу й оцінити впевненість в отриманих висновках. При цьому розрізняють два види залежності – функціональну й статистичну (кореляційну).

Поняття функціональної залежності

Будемо вважати, що між двома показниками X й Y існує функціональна залежність (взаємозв'язок), при якій кожному значенню одного з них відповідає одне строго визначене значення іншого.

Поняття кореляційної залежності і її спрямованості

Будемо вважати, що між двома показниками Х и Y існує кореляційна залежність (взаємозв'язок), при якій зі зміною одного показника змінюється й інший, але кожному значенню показника Х можуть відповідати різні, заздалегідь непередбачені значення показника Y, і навпаки.

Для виявлення спрямованості впливу одного показника на інший введені поняття позитивного й негативного зв'язку.

Якщо зі збільшенням (зменшенням) одного показника збільшуються (зменшуються) значення іншого, то такий кореляційний зв'язок називається прямий або позитивний.

Якщо зі збільшенням (зменшенням) одного показника зменшуються (збільшуються) значення іншого, то такий кореляційний зв'язок називається зворотним або негативним.

2. Кореляційні поля і їх використання в попередньому аналізі кореляційного зв'язку

При постановці питання про кореляційну залежність між двома статистичними ознаками Х и Y проводять експеримент із паралельною реєстрацією їх значень.

Приклад 1: визначити, чи залежить результат стрибка в довжину з розбігу (показник Х) від величини кінцевої швидкості розбігу (показник Y). Для відповіді на це питання паралельно з реєстрацією результату Х кожного стрибка спортсмена або групи спортсменів реєструють і величину кінцевої швидкості розбігу Y. Припустимо, вони такі:

 

Таблиця 1

Показники кінцевої швидкості розбігу та довжини стрибка

 

Показник
x (см)
y (м/с)	10,7	10,5	10,1	9,8	10,1	10,5	9,1	9,6

 

Представимо таблицю 1 у вигляді графіка в прямокутній системі координат, де на горизонтальній осі будемо відкладати довжину стрибка (Х), а на вертикальній – величину кінцевої швидкості розбігу в цьому стрибку (Y) .

Побудувати графік кореляційного поля.

 

 

Рис. 1. Графік кореляційного поля

 

Будемо називати кореляційним полем зону розкиду отриманих точок на графіку. Візуально аналізуючи кореляційне поле на рис. 1, можна помітити, що воно немовби витягнуте вздовж уявної прямої лінії. Така картина характерна для так званого лінійного кореляційного взаємозв'язку між показниками. При цьому можна припустити, що зі збільшенням кінцевої швидкості розбігу збільшується й довжина стрибка, і навпаки. Тобто, між розглянутими показниками спостерігається прямий (позитивний) взаємозв'язок.

Крім цього, за кореляційним полем можна приблизно судити про тісноту (щільність) кореляційного зв'язку, якщо цей зв'язок існує. Тут говорять: чим менше точки розкидані біля уявної усередненої лінії, тим тісніше кореляційний зв'язок між розглянутими показниками.

Візуальний аналіз кореляційних полів допомагає розібратися в сутності кореляційного взаємозв'язку, дозволяє висловити припущення про наявність, спрямованість і тісноту зв'язку. Але точно сказати, є зв'язок між ознаками чи ні, лінійний зв'язок або криволінійний, тісний зв'язок (достовірний) або слабкий (недостовірний), за допомогою цього методу не можна. Найбільш точним методом виявлення й оцінки лінійного взаємозв'язку між показниками є метод визначення різних кореляційних показників за статистичним даними.

 

3. Коефіцієнти кореляції і їх властивості

Часто для визначення вірогідності взаємозв'язку між двома ознаками(Х, Y) використовуютьпараметричний коефіцієнт кореляції
Пірсона (або непараметричний (ранговий) коефіцієнт кореляції Спірмена). Величина показника кореляційного зв'язку визначається за наступною формулою:

,

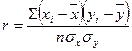де: х – статистичні дані показника х,

у – статистичні дані показника у.

 

Коефіцієнт має такі потужні ознаки:

1. На підставі коефіцієнтів кореляції можна судити тільки про прямолінійний кореляційний взаємозв'язок між показниками. Про криволінійний зв'язок з їх допомогою нічого сказати не можна.

2. Значення коефіцієнтів кореляції є безрозмірна величина, що не може бути менше -1 і більше +1, тобто -1≤r ≤+1.

3. Якщо значення коефіцієнтів кореляції дорівнюють нулю, тобто
r_ху = 0, то зв'язок між показниками відсутній.

4. Якщо значення коефіцієнтів кореляції негативні, тобто r_ху < 0, то зв'язок між показниками Х и Y зворотний.

5. Якщо значення коефіцієнтів кореляції позитивні, тобто r_ху > 0, то зв'язок між показниками Х и Y прямий (позитивний).

6. Якщо коефіцієнти кореляції приймають значення +1 або –1, тобто r_ху = ± 1, то зв'язок між ознаками Х и Y лінійний (функціональний).

Крім перерахованих загальних властивостей, у коефіцієнтів кореляції є й різниця. Головна відмінність полягає в тому, що коефіцієнт Пірсона r_ху може бути використаний тільки у випадку нормальності розподілу ознак Х и Y, а коефіцієнт Спірмена – для ознак з будь-яким видом розподілу.

Якщо розглянуті ознаки мають нормальний розподіл, то доцільніше визначати наявність кореляційного зв'язку за допомогою коефіцієнта Пірсона, тому що в цьому випадку він буде мати меншу погрішність, ніж коефіцієнт Спірмена.

ХIД РОБОТИ

1. Будуємо таблицю, куди заносимо значення показників х та у.

Показники х:

Показники у:

2. Вираховуємо суму та середнє арифметичне значення показників х та у.

3. Вираховуємо ( ), ( ).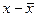

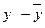4. Здійснюємо розрахунки 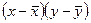та знаходимо суму 6 ст.

5. Підносимо до квадрату і та підраховуємо Σ ст. 7, 8.

 

Таблиця 2

№ з/п	х	у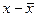
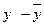
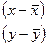
… Σ Сер.

 

6. Вираховуємо середнє квадратичне відхилення (σ).

 

 

 

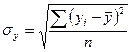7. Вирахувати коефіцієнт кореляції Пірсона (r_ху):

 

 

 

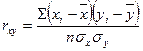
8. Висновок.

 

 

Література

1. Иванов В.С. Основы математической статистики. – М.: ФиС, 1990. – С. 22-30.

2. Начинская С.В. Основы математической статистики. – К.: Вища школа, 1987. – 190 с.

3. Спортивная метрология /Под ред. В.М.Зациорского. – М.: ФиС, 1982. – 256 с.

Лабораторна робота №3

 

ВИРАХУВАННЯ КОРЕЛЯЦІЙНОГО ВІДНОШЕННЯ

 

Мета: навчитись визначати ступінь взаємозв’язку між показниками при нелінійній формі залежності.

 

 

ТЕОРЕТИЧНІ ВІДОМОСТІ

Для оцінки ступеня взаємозв’язку при нелінійній формі залежності і вимірах у шкалах інтервалів та відносин використовують кореляційне відношення (η – ета).

При лінійній залежності значення кореляційного відношення за абсолютною величиною співпадає з коефіцієнтом кореляції.

 

 

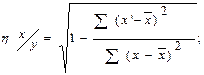де η _у/х , η _х/у – кореляційні відношення;

х та у – варіанти показників х та у;

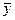та – середні арифметичні значення показників;

х’ та у’ – приватні середні показників.

 

 

ХІД РОБОТИ

Для визначення приватних середніх х’ та у’ знаходять середнє арифметичне другого показника серед відповідних їм однакових варіантів першого показника.

Кореляційне відношення завжди позитивне, не виходить за межі від 0 до 1.

1. Будуємо таблицю №1 і заносимо дані (в табл. 7 стовпчиків, 10 показників).

 

Показники х: 45, 45, 50, 51, 51, 51, 51, 53, 53, 55.

Показники у: 7, 8, 11, 6, 5, 7, 9, 12, 3, 5.

Таблиця 1

№ з/п	х	у	у’
…
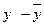
Σ
Сер.

 

2. Знаходимо суму Σ у, потім середнє арифметичне значення у.

3. Знаходимо приватне середнє показника у’

(знаходимо однакові варіанти першого показника (х = 45, 45), далі їм відповідають показники другого признака (у = 7, 8) і знаходимо середнє арифметичне другого показника у (у = (7+8) : 2 = 7,5).

4. Потім знаходимо (у’ = 5 – у = 7,3 = 0,2).

5. Також вираховуємо .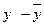

6. Далі підносимо до квадрату: та .

7. Знаходимо суму та суму .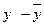

8.

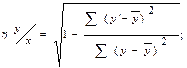Підставляємо у формулу значення.

 

9. Висновок 1: η _у/х складає 0,844; тому залежність показника у від показника х висока.

10. Будуємо таблицю №2, але для показника х; тут замінюємо у на х.

Показники у записуємо по ранжиру.

 

Таблиця 2

№ з/п	у	х	х'
…
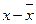
Σ
Сер.

 

11. Знаходимо суму Σ х, потім середнє арифметичне значення х.

12. Знаходимо приватне середнє показника х'

13. Потім знаходимо .

14. Також вираховуємо .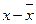

15. Підносимо до квадрату: та .

16. Знаходимо суму Σ та Σ .

17. Підставляємо у формулу значення.

 

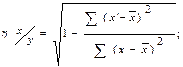Висновок 2: η _х/у = ,363; залежність показника х (динамометрія) від показника у є слабкою, тобто другий показник у (підтягування) впливає більше на показник х , ніж х на у.

 

Література

 

1. Иванов В.С. Основы математической статистики. – М.: ФиС, 1990. – С. 22-30.

2. Начинская С.В. Основи математической статистики. – К.: Вища школа, 1987. – 190 с.

Лабораторна робота №4

 

ВИРАХУВАННЯ ПРИВАТНОГО КОЕФІЦІЄНТА КОРЕЛЯЦІЇ

 

Мета: навчитись знаходити ступінь взаємозв’язку між показниками (х та у) при виключенні впливу на них деякого третього показника (z).

 

 

ТЕОРЕТИЧНІ ВІДОМОСТІ

На взаємозв’язок двох показників впливають різні фактори. Тому на практиці часто виникає необхідність оцінити взаємозв’язок показників х та у при незмінності всіх інших показників (z, q та інші).

У таких випадках вираховують приватний (або парціальний) коефіцієнт кореляції: r _ху∙z. Коефіцієнт r _ху∙zдозволяє оцінити взаємозв’язок х та у при виключенні впливу на нього показника z. Приватний коефіцієнт кореляції змінюється в межах від –1 до +1 (як і звичайний парний лінійний коефіцієнт кореляції).

Вираховується за формулою:

 

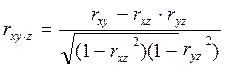
де r _ху, r _хz, r _уz – парні лінійні коефіцієнти кореляції.

 

 

ХІД РОБОТИ

1. Будуємо таблицю і заносимо показники (в табл. 13 стовпчиків).

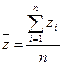
2. Знаходимо Σ х, у, z; потім середні арифметичні значення:

 

Таблиця 1

№

х

у

z

…

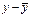
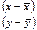
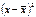
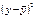
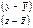
Σ

 

3. Вираховуємо середнє квадратичне відхилення σ_х, σ_у,σ_z.

 

 

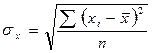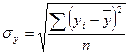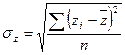4. Вираховуємо парні лінійні коефіцієнти кореляції: r _ху, r _хz, r _уz:

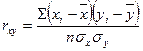
5. Вираховуємо приватний коефіцієнт кореляції: r _ху∙z.

6. Висновок.

Література

 

1. Иванов В.С. Основы математической статистики. – М.: ФиС, 1990. – С. 22-30.

2. Лакин Г.Ф. Биометрия. – М.: Высшая школа, 1973. – 343 с.

Лабораторна робота №5

 

ВИРАХУВАННЯ МНОЖИННОГО КОЕФІЦІЄНТА КОРЕЛЯЦІЇ

 

Мета: навчитись знаходити множинний коефіцієнт кореляції та практично його застосовувати у фізичному вихованні і спорті.

 

ТЕОРЕТИЧНІ ВІДОМОСТІ

Для дослідження щільності взаємозв’язку між показником х і деяким набором інших показників використовують множинний коефіцієнт кореляції, який позначається R _хуz.

При оцінці взаємовпливу показників у і z на показник х значення множинного коефіцієнта кореляції вираховують за формулою:

 

 

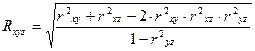
Звернемо увагу, що множинний коефіцієнт кореляції змінюється в межах від 0 до +1 (негативних значень немає).

 

ХІД РОБОТИ

1. Використовуємо варіаційні ряди з роботи №4, дані х, у, z.

2. Дані r _ху, r _хz, r _уz підносимо до квадрата.

3. Отримані r _ху², r _хz², r _уz² підставляємо у формулу і вираховуємо множинний коефіцієнт кореляції.

4. Висновок.

 

Література

 

1. Лакин Г.Ф. Биометрия. – М.: Высшая школа, 1973. – 343 с.

2. Начинская С.В. Основы математической статистики. – К.: Вища школа, 1987. – 190 с.

3. Спортивная метрология / Под ред. В.М. Зациорского. – М.: ФиС, 1982. – 256 с.

Лабораторна робота №6

 

ВИМІРЮВАННЯ ВЗАЄМОДІЇ ТІЛА СПОРТСМЕНА З ОПОРОЮ МЕТОДОМ ТЕНЗОДИНАМОМЕТРІЇ

 

Мета: ознайомитись з методикою вимірювання реакції спортсмена з опорою при виконанні фізичних вправ в різних видах спорту.

 

Завдання:

1. Ознайомитись зі складом електротензодинамометричного комплексу.

2. Здобути навички техніки проведення вимірювань та реєстрації опорних характеристик.

 

Прилади та інвентар:

1. Електротензодинамометричний комплекс “Модуль”, який складається з тензодинамометричної платформи ПД-3А та блоку вторинних перетворювачів БВП-2.

2. Комп’ютер.

3. Спеціальне програмне забезпечення.

 

 

ТЕОРЕТИЧНІ ВІДОМОСТІ

Метод електротензодинамографії(від лат. tenzor – напружую, розтягую) дозволяє реєструвати та вимірювати зусилля, які розвиває людина під час взаємодії з опорою та іншими об'єктами навколишнього середовища, які мають певну масу.

Усі тіла під дією прикладених до них сил деформуються, а вели­чина деформації кожного такого пружного тіла пропорційна прикладеному зусиллю. Внаслідок виконання руху лю­дина здійснює механічний вплив на ту поверхню опори, відносно якої вона переміщується, наприклад бігові доріжки та різні спортивні снаряди, які під час цієї взаємодії дефор­муються. Щоб виміряти величини зусиль, що розвиває людина, зас­тосовують спеціальні тензодатчики, які перетворюють величини ме­ханічної деформації на електричний сигнал. В основі роботи кожно­го такого тензодатчика лежить явище тензоефекту – властивість дея­ких матеріалів змінювати електричний опір під впливом деформації. Такий датчик – електричний провідник – наклеюється на пружний силовимірювальний елемент, що сприймає зусилля. При деформації пружного силовимірювального елемента відбувається деформація і наклеєного на нього тензодатчика, внаслідок цього на якусь величи­ну і змінюється електричний опір тензодатчика.

Тензодинамометрична апаратура застосовується для визначення силових характеристик рухів і вивчення на їх основі динамічної структури рухових дій та ефективність рухів у цілому. При цьому залежно від завдань розрізняють універсальні та окремі методики електротензодинамографії (ЕТДГ).

Універсальні методики ЕТДГ. В теперішній час найпоширенішими є тензодинамометричні платформи. Найбільш відомі з них – електротензодинамометричний комплекс “Модуль” площею 0,56 м² виробництва ВІСТІ (Росія) та тензоплатформа фірми KISTLER (Німеччина), що має площу 0,48 м³. Такі платформи можуть розташовуватися на доріжках стадіонів, під важкоатлетичними помостами, у місцях відштовхування людини від опори при виконанні різних рухових дій. За допомогою динамографічних платформ, наприклад, вимірюються біомеханічні параметри опорних взаємодій людини у процесі ходьби, бігу, стрибків у довжи­ну та висоту, стрибків на лижах з трампліна, стрибків у воду, а також у гімнастиці, акробатиці.

Доцільним є одночасне використання разом з динамографічною платформою інших методів реєстрації, наприклад вимірювання кінематичних характеристик рухів методами гоніометрії, телекіноциклографії та відео аналізу.

Приватні методики ЕТДГ. Для різноманітних рухів людини передбачається використовувати різні вимірювальні пристрої для запису зусиль, що розвиваються при взаємодії його тіла з опорою. Основною умовою при проектуванні силовимірювальних пристроїв є чітке пере­давання усього зусилля на балку, до котрої приклеєні тензодатчики. Наприклад, для таких видів спорту, як велосипедний, ковзанярський, силовимірювачі встановлюються на педалі велосипеда, під усю підошву черевика. Для вимірювання взаємодії у плаванні можна сконструювати рукавички з тонким силовимірювачем на долоні й за допомогою такого пристрою фіксувати силу, частоту та інтенсивність гребка. У веслуванні датчики найчасті­ше наклеюють на весло. Для вивчення ударів у видах спорту, наприк­лад, таких, як теніс, датчики можна наклеювати на ракетку (у ший­ці). Те саме можна робити і у стрибках у воду, наклеюючи датчики на дошку перед середньою опорою. У гімнастиці датчики наклеюють також на кільця, бруси, перекладину, опорний місток. У важкій атле­тиці датчик краще розташовувати безпосередньо на штанзі. Тензодат­чики укріплюють у підметку бігового взуття легкоатлетів або розташо­вують їх на біговій доріжці, у стартових колодках. Часто чутливий тензоелемент роблять зйомним, що дає змогу використовувати його на різних спортивних снарядах. Інформативність отриманих результа­тів набагато зростає у разі синхронного запису тензодинамограми, гоніограми та кіно- і відеозйомки досліджуваного руху.

Конструкція універсального електротензометричного комплексу.

До електротензодинамометричного комплексу входять: тензоплатформа ПД-ЗА; блок вторинного перетворення БВП-2; універсальна плата перетворення електричних сигналів; комп'ютер з програмним забезпеченням; принтер.

Тензодинамограма – крива зміни силових параметрів опорних характеристик рухів.

 

ХІД РОБОТИ

1. Ознайомитись з інструкцією користувача.

2. Включити автоматизований тензодинамометричний комплекс.

3. Провести перевірку показників комплексу за віссю Z.

4. Виконати реєстрацію данамограми стрибка вгору поштовхом двома ногами на максимальну висоту. Зафіксувати тензодинамометричні показники.

6. Виконати дослідження в реальному масштабі часу біомеханічних характеристик опорних реакцій окремих спортсменів при виконанні різних вправ (старт легкоатлета, нападаючий удар та блокування волейболіста, кидок м’яча у баскетболі, удар м’яча у футболі, штовхання ядра, метання снарядів).

7. Виконати роздрукування індивідуальних тензодинамограм.

8. Виконати порівняння тензодинамограм різних спортсменів.

 

 

Рис. 1. Тензодинамограма виконання нападаючого удару

 

 

9. Здійснити математичну обробку результатів тензодинамограм методом середніх величин.

10. Висновок з результатів виконання лабораторної роботи.

 

 

Література

 

1. Біомеханіка спорту /Під заг. ред. А.М.Лапутіна. – К.: Олімпійська література, 2005. – 319 с.

2. Лапутин А.Н. Олимпийскому спорту – высокие технологии. – К.: Знання, 1999. – 164 с.

3. Лапутин А.Н. Практическая биомеханика. – К.: Науковий світ, 2000. – 298 с.

Лабораторна робота №7

 

ВИМІРЮВАННЯ УМОВ РІВНОВАГИ ТІЛА СПОРТСМЕНА
МЕТОДОМ СТАБІЛОГРАФІЇ

 

Мета: ознайомитись з методикою вимірювання здібності до збереження рівноваги спортсменами в різних положеннях.

 

Завдання:

1. Ознайомитись зі складом стабілографічного комплексу.

2. Здобути навички техніки проведення вимірювань та реєстрації стабілографічних характеристик.

 

Прилади та інвентар:

1. Стабілографічний комплекс “Модуль”, який складається з тензодинамометричної платформи ПД-3А та блоку вторинних перетворювачів БВП-2.

2. Комп’ютер.

3. Спеціальне програмне забезпечення.

 

 

ТЕОРЕТИЧНІ ВІДОМОСТІ

Трудова та спортивна рухова діяльність у багатьох випадках вимагає від людини здатності досить економічно й з високим робочим ефектом утримувати певні робочі пози, видозмінювати їх, зберігаючи рівновагу свого тіла в просторі. Біомеханічні раціональні рухи та пози часто визначають кінцевий результат тієї чи іншої діяльності людини. Ще в минулому столітті угорський лікар Ромберг ввів у клінічну практику спостереження за вертикальним положенням тіла та розробив методики оцінки ступеня коливання тіла й тремору кінцівок. Їм було доведено, що оцінка вертикального положення тіла є важливим індикатором функціонального стану організму людини, її здоров’я.

У практиці спорту часто зустрічаються різні статичні положення та пози. До таких статичних положень належать різні стійки, виси, упори в спортивній гімнастиці, стартові положення в легкій атлетиці, плаванні та інших видах спорту, пози важкоатлетів, стрільців тощо. Роль цих положень та поз як елементів спортивної техніки може бути зовсім різною, якщо розглядати їх основні три фази – початкову, проміжну та кінцеву. Залежно від того, до якої з цих фаз належить досліджувана статична поза, можна конкретно оцінити її роль в ефективному розв'язанні рухового завдання. Про значну роль статичних положень та поз у спорті свідчить і той факт, що в змаганнях за суддівськими правилами регламентується фіксація статичних поз.

Процес збереження положення та пози тіла – це складний процес управління та регуляції. Для оцінки умов рівноваги тіла людини нині досить широко застосовується методика стабілографії. Останнім часом ця методика, окрім дослідження власне біомеханічних основ стійкості, застосовується також для вивчення функціонального стану організму людини, стерпності до навантажень статичного та динамічного характеру, оцінки координаційних можливостей людини.За всієї складності електронного комплексу апаратури, що використовується в методиці стабілографії, людина за час вимірювань не обтяжується прикріпленням датчиків до біоланок її тіла: їй лише необхідно стати на стабілографічну платформу та виконати відповідний контрольний тест.

Методика, що забез­печує можливість кількісного та якісного аналізу стійкості стояння називаєтьсястабілографією.Крива зміни координат ЗЦМ ті­ла при збереженні стійкості стояння називається стабілограмою.

Основними кількісними критеріями статичних поз є показники амплітудних, частотних коливань в сагітальній і фронтальній площинах.

Оптимальними взаємозв’язками структурних елементів є: довгий час фіксації поз та положень тіла, оптимальні амплітуда, частота і період коливань, малий час стабілізації стійкості, сформований темпоритм у динамічних рівновагах. Співвідношення двох провідних компонентів СДС – амплітуди і чистоти коливань тіла – має свої специфічні особливості для різноманітних спортивних спеціалізацій та спортсменів різної спортивної кваліфікації.

За підсумками стабілографічних досліджень роблять індивідуальні висновки про рівень та динаміку СДС в структурі функціональної і технічної підготовленості спортсменів.

ХІД РОБОТИ

1. Включити автоматизований тензодинамометричний комплекс

2. Провести перевірку показників комплексу за віссю Х та У.

3. Виконати реєстрацію стабілограми в стандартному тесті на стійкість (проба Ромберга).

 

Рис. 2. Приклад стабілограми проби Ромбегра

 

4. Виконати роздрукування індивідуальних стабілограм.

5. Виконати порівняння стабілограм різних спортсменів.

6. Здійснити математичну обробку результатів стабілограм навчальної групи методом середніх величин.

7. Висновок з результатів виконання лабораторної роботи.

 

Література

1. Біомеханіка спорту /Під заг. ред. А.М.Лапутіна. – К.: Олімпійська література, 2005. – 319 с.

2. Лапутин А.Н. Олимпийскому спорту – высокие технологии. – К.: Знання, 1999. – 164 с.

3. Лапутин А.Н. Практическая биомеханика. – К.: Науковий світ, 2000. – 298 с.