Уравнение Шредингера. Границы его применимости. Решение уравнения Шредингера в стационарном случае.

Толкование волн де Бройля и соотношение неопределенностей Гейзенберга привели к выводу, что уравнением движения в квантовой механике, описывающей движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно быть уравнением относительно волновой функции 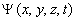, т.к. именно величина 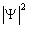осуществляет вероятность пребывания частицы в момент времени t в объеме dV, т.е. в области с координатами x и , y и , z и . Т.к. искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны.

Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Шредингером.
Разработал теорию движения микрочастиц – волновую механику, построил квантовую теорию возмущений – приближенный метод в квантовой механике. За создание волновой механики удостоен Нобелевской премии.

Уравнение Шредингера не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом получаемых с его помощью результатов, что, в свою очередь, придает ему характер закона природы.

Уравнение Шредингера в общем виде записывается так:

(4.4.1)

где m – масса частицы,i² – мнимая единица, – оператор Лапласа 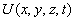– потенциальная энергия частицы в силовом поле, в котором она движется, Ψ – искомая волновая функция.

Если силовое поле, в котором движется частица, потенциально, то функция U не зависит явно от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шредингера распадается на два сомножителя, один из которых зависит только от координаты, а другой – только от времени:

.

(4.4.2)

Здесь E – полная энергия частицы, которая в случае стационарного поля остается постоянной. Чтобы убедиться в справедливости выражения 4.4.2, подставьте его в выражение (4.4.1), и вы получите уравнение Шредингера для стационарных состояний:

,

.

(4.4.3)

Уравнение Шредингера можно записать в виде .

В этом уравнении – оператор Гамильтона, равный сумме операторов . Гамильтониан является оператором энергии E.

В квантовой механике другим переменным также и динамическим сопоставляются операторы. Соответственно рассматривают операторы координат, импульса, момента импульса и т.д.