Вектор ускорения точки

ВЕКТОР УСКОРЕНИЯ ТОЧКИ

 

Рисунок 5

 

Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки.

Пусть в некоторый момент времени t движущаяся точка находится в положении М и имеет скорость v̅, а в момент t₁ приходит в положение М₁ и имеет скорость v̅₁ (рис. 5). Тогда за промежуток времени 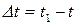скорость точки получает приращение .

Для построения вектора Δv̅ отложим от точки М вектор, равный v̅₁ и построим параллелограмм, в котором диагональю будет v̅₁, a одной из сторон v̅. Тогда, очевидно, вторая сторона и будет изображать вектор Δv̅. Заметим, что вектор Δv̅ всегда направлен в сторону вогнутости траектории.

Отношение приращения вектора скорости Δv̅ к соответствующему промежутку времени Δt определяет вектор среднего ускорения точки за этот промежуток времени:

(9)

 

Вектор среднего ускорения имеет то же направление, что и вектор Δv̅, т. е. направлен в сторону вогнутости траектории.

Ускорением точки в данный момент времени t называется век-

векторная величина a̅, к которой стремится среднее ускорение a̅_ср при

стремлении промежутка времени Δt к нулю:

 

 

или, с учетом равенства (8),

 

 

Следовательно, вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.

Размерность ускорения L/T², т. е. длина/(времяJ; в качестве единицы измерения применяется обычно м/с².

Из формулы (10) следует также, что вектор ускорения точки a̅ равен отношению элементарного приращения вектора скорости dv̅ к соответствующему промежутку времени dt.

Найдем, как располагается вектор a̅ по отношению к траектории точки. При прямолинейном движении вектор a̅ направлен вдоль прямой, по которой движется точка. Если траекторией точки является плоская кривая, то вектор ускорения a̅, так же как и вектор a̅_ср, лежит в плоскости этой кривой и направлен в сторону ее вогнутости.

Если траектория не является плоской кривой, то вектор a̅_ср направлен в сторону вогнутости траектории и лежит в плоскости, проходящей через касательную к траектории в точке М и прямую, параллельную касательной в соседней точке М₁ (рис. 5). В пределе, когда точка М₁ стремится к М, эта плоскость занимает положение так называемой соприкасающейся плоскости, т. е. плоскости, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении движущейся точки (для пространственной кривой, например, для винтовой линии, в каждой точке кривой будет своя соприкасающаяся плоскость; для плоской кривой соприкасающаяся плоскость совпадает с плоскостью этой кривой и является общей для всех ее точек). Следовательно, в общем случае вектор ускорения a̅ лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой. Вопрос об определении модуля ускорения будет рассмотрен в следующем разделе.