Способы задания движения точки

СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ

Для задания движения точки можно применять один из следующих трех способов: 1) векторный, 2) координатный, 3) естественный.

1. Векторный способ задания движения точки. Пусть точка М движется по отношению к некоторой системе отсчета Oxyz. Положение этой точки в любой момент можно определить, задав ее радиус-вектор , проведенный из начала координат О в точку М (рис. 1).

При движении точки М вектор будет с течением времени изменяться и по модулю, и по направлению. Следовательно, является переменным вектором (вектором-функцией), зависящим от аргумента t:

Равенство (1) и определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки.

Геометрическое место концов вектора , т. е. годограф этого вектора, определяет траекторию движущейся точки.

Аналитически, как известно, вектор задается его проекциями на координатные оси. В прямоугольных декартовых координатах для вектора будет: r_x=x, r_y=y, r_z=z (см. рис. 1), где х, у, z — декартовы координаты точки. Тогда, если ввести единичные векторы (орты) 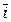, , координатных осей, получим для выражение

Рисунок 1

Следовательно, зависимость (2) от t будет известна, если будут заданы координаты х, у, z точки как функции времени. Такой способ задания движения точки (координатный) рассмотрим ниже. Вектор может быть задан, как известно, и иными способами, например его модулем и углами с осями или проекциями на оси других систем координат. Для получения общих формул, не зависящих от того, как конкретно задан вектор , будем исходить из векторного закона движения, представленного равенством (2).

2. Координатный способ задания движения точки. Положение точки можно непосредственно определять ее декартовыми координатами х, у, z, которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т. е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т. е. знать зависимости

Уравнения (3) представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения. Если движение точки происходит все время в одной и той же плоскости, то, приняв эту плоскость за плоскость Оху, получим в этом случае два уравнения движения:

Наконец, при прямолинейном движении точки, если вдоль ее траектории направить координатную ось Ох, движение будет определяться одним уравнением (законом прямолинейного движения точки)

Уравнения (3) и (4) представляют собой одновременно уравнения траектории точки в параметрической форме, где роль параметра играет время t. Исключив из уравнений движения время t, можно найти уравнение траектории в обычной форме, т. е. в виде, дающем зависимость между координатами точки.

Пример. Пусть движение точки в плоскости Оху дано уравнениями:

где х, у выражены в сантиметрах; t— в секундах.

По этим уравнениям можно найти, что в момент времени t = 0 точка находится в положении М₀(0, 0), т. е. в начале координат, в момент t = lc — в положении M₁ (2,12) и т д. Таким образом, уравнения (а) действительно определяют положение точки в любой момент времени. Давая t разные значения и изображая соответствующие положения точки на рисунке, можем построить ее траекторию.

Другим путем траекторию можно найти, исключив t из уравнении (а). Из первого уравнения находим t = x/2 и, подставляя это значение t во второе уравнение, получаем y = x². Следовательно, траекторией точки является парабола с вершиной в начале координат и осью, параллельной оси Оу. Другие примеры определения траектории точки будут рассмотрены на практических занятиях.

Рисунок 2

3. Естественный способ задания движения точки. Естественным (или траекторным) способом задания движения удобно пользоваться в тех случаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ является траекторией точки М при ее движении относительно системы отсчета Oxyz (рис. 2). Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицательное направления отсчета (как на координатной оси). Тогда положение точки М на траектории будет однозначно определяться криволинейной координатой s, которая равна расстоянию от точки О' до точки М, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M_l, М₂,. . ., следовательно, расстояние s будет с течением времени изменяться. Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость

Уравнение (6) и выражает закон движения точки М вдоль траектории.

Таким образом, чтобы задать движение точки естественным способом, надо задать: 1) траекторию точки; 2) начало отсчета на траектории с указанием положительного и отрицательного направлений отсчета; 3) закон движения точки вдоль траектории в виде s = f(t).

Заметим, что величина s в уравнении (6) определяет положение движущейся точки, а не пройденный ею путь. Например, если точка, двигаясь из начала О', доходит до положения М₁ (рис. 2), а затем, перемещаясь в обратном направлении, приходит в положение М, то в этот момент ее координата s = O'M, а пройденный за время движения путь будет равен O'M₁ + M₁M, т. е. не равен s.