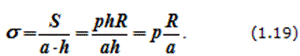Распределенные нагрузки
Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.
Размерность для линейной нагрузки - Н/м, для нагрузки распределенной по площади - Н/м2, для объемной (например при учете собственного веса элементов конструкции) - Н/м3.
Например, на рисунке 1.23, а приведена равномерно распределенная по длине AB нагрузка интенсивностью q , измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой
Q = q⋅ AB [Н],
приложенной в середине отрезка AB . На рисунке 1.23, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой
Q = 1/2 qmax⋅ AB,
приложенной в точке C , причем AC = 2/3 AB .
В произвольном случае, зная функцию q(x) (рисунок 1.23, в), рассчитываем эквивалентную силу

Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).



Рисунок 1.23
Примером может служить расчет усилий, разрывающих стенки баллона со сжатым газом. Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м]; R – радиус трубы, 2α – центральный угол, ось Ox – ось симметрии (рисунок 1.24).
Выделим элемент сектора с углом ∆φ и определим силу ∆Q , действующую на плоский элемент дуги:
∆Q = q⋅ ∆l = q⋅ R⋅ ∆φ. (1.14)

Рисунок 1.24
Проекция этой силы на ось Ox будет
∆Qx = q⋅ R⋅ ∆φ⋅ cosφ . (1.15)
В силу симметрии элемента трубы (с дугой AB ) относительно оси Ox проекция результирующей силы на ось Oy
Qy = 0, т.е. Q = Qx , (1.16)

где АВ– хорда, стягивающая концы дуги.
Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует нагрузка интенсивностью q = p [Н/м2]. Если цилиндр рассечен по диаметру (рисунок 1.25), то равнодействующая этих сил равна F = q⋅d⋅ h ( d – внутренний диаметр);F = p⋅ 2R⋅ h .
Разрывающие баллон по диаметру усилия:
S1 = S2 = S; 2S = F; S = phR. (1.18)
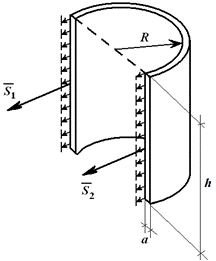
Рисунок 1.25
Если принять a – толщина стенки, то (пренебрегая усилиями в крышке и дне цилиндра) растягивающее напряжение в стенке равно