Основные формулы и законы
Общие методические указания
При решении и оформлении задач необходимо соблюдать следующие требования:
1. Записать краткое условие задачи, выразить все известные величины в одной и той же системе единиц (как правило, в СИ). При необходимости ввести дополнительные постоянные физические величины.
2. Решение задач следует сопровождать краткими, но исчерпывающими объяснениями. При необходимости дать чертеж или график.
3. Решать задачу надо в общем виде, т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. Произвести вычисления по расчетной формуле с соблюдением правил приближенных вычислений.
Результаты контроля аудиторной и самостоятельной работы студентов на практических занятиях учитываются лектором при приеме экзаменов и дифференцированных зачетов.
Электростатика
Основные формулы и законы
· Закон Кулона
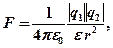
где 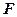 – модуль силы взаимодействия двух точечных зарядов
– модуль силы взаимодействия двух точечных зарядов 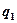 и
и 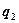 ;
;  – расстояние между зарядами;
– расстояние между зарядами;  - электрическая постоянная,
- электрическая постоянная,  -диэлектрическая проницаемость среды, в которой находятся заряды (для вакуума
-диэлектрическая проницаемость среды, в которой находятся заряды (для вакуума  )
)
· Напряженность и потенциал электростатического поля
 ;
;  , или
, или  ,
,
где 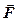 – сила, действующая на точечный положительный заряд
– сила, действующая на точечный положительный заряд 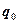 , помещенный в данную точку поля;
, помещенный в данную точку поля; 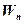 – потенциальная энергия заряда
– потенциальная энергия заряда 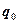 ;
;  – работа по перемещению заряда
– работа по перемещению заряда 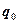 из данной точки поля в бесконечность.
из данной точки поля в бесконечность.
· Напряженность и потенциал электростатического поля, создаваемого точечным зарядом  на расстоянии
на расстоянии  от него
от него
 ;
;  .
.
· Поток вектора напряженности через площадку 
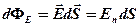 ,
,
где  – вектор, модуль которого равен
– вектор, модуль которого равен  , а направление совпадает с нормалью
, а направление совпадает с нормалью  к площадке;
к площадке; 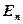 – составляющая вектора
– составляющая вектора 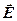 по направлению нормали
по направлению нормали  к площадке.
к площадке.
· Поток вектора напряженности через произвольную поверхность 
 .
.
· Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции (наложения) электростатических полей)
 ;
;  ,
,
где  ,
, 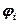 – соответственно напряженность и потенциал поля, создаваемого зарядом
– соответственно напряженность и потенциал поля, создаваемого зарядом  ,
,  – число зарядов, создающих поле.
– число зарядов, создающих поле.
· Связь между напряженностью и потенциалом электростатического поля
 , или
, или  ,
,
где 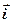 ,
,  ,
, 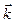 – единичные векторы координатных осей.
– единичные векторы координатных осей.
· В случае поля, обладающего центральной или осевой симметрией,
 .
.
· Для однородного поля (поля плоского конденсатора)
 ,
,
где  - разность потенциалов между пластинами конденсатора,
- разность потенциалов между пластинами конденсатора, 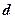 - расстояние между ними.
- расстояние между ними.
· Электрический момент диполя (дипольный момент)
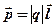 ,
,
где 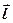 – плечо диполя (векторная величина, направленная от отрицательного заряда к положительному).
– плечо диполя (векторная величина, направленная от отрицательного заряда к положительному).
· Линейная, поверхностная и объемная плотность зарядов, т.е. заряд, приходящийся соответственно на единицу длины, площади и объема:
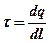 ;
;  ;
; 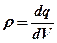 .
.
· Теорема Гаусса для электростатического поля в вакууме
 ,
,
где  – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности
– алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности  ;
;  – число зарядов;
– число зарядов;  – объемная плотность зарядов.
– объемная плотность зарядов.
· Напряженность поля, создаваемая равномерно заряженной бесконечной плоскостью,
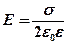 .
.
· Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом 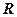 с зарядом
с зарядом  на расстоянии
на расстоянии  от центра сферы,
от центра сферы,
 ;
;  при
при  (внутри сферы);
(внутри сферы);
 ;
;  при
при  (вне сферы).
(вне сферы).
· Напряженность поля, создаваемого равномерно заряженной бесконечной цилиндрической поверхностью радиусом 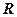 на расстоянии
на расстоянии  от оси цилиндра,
от оси цилиндра,
 при
при  (внутри цилиндра);
(внутри цилиндра);
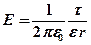 при
при  (вне цилиндра).
(вне цилиндра).
· Работа, совершаемая силами электростатического поля при перемещении заряда 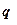 из точки 1(потенциал
из точки 1(потенциал  ) в точку 2 (потенциал
) в точку 2 (потенциал  ),
),
 , или
, или 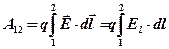 ,
,
где 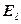 – проекция вектора
– проекция вектора 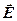 на направление элементарного перемещения
на направление элементарного перемещения  .
.
· Вектор поляризации диэлектрика
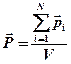 ,
,
где  – объем диэлектрика;
– объем диэлектрика;  – дипольный момент
– дипольный момент  -й молекулы,
-й молекулы,  – число молекул.
– число молекул.
· Связь между вектором поляризации и напряженностью электростатического поля в той же точке внутри диэлектрика
 æe0
æe0 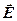 ,
,
где æ – диэлектрическая восприимчивость вещества.
· Связь диэлектрической проницаемости  с диэлектрической восприимчивостью æ
с диэлектрической восприимчивостью æ
e = 1 + æ.
· Связь между напряженностью  поля в диэлектрике и напряженностью
поля в диэлектрике и напряженностью  внешнего поля
внешнего поля
 .
.
· Связь между векторами электрического смещения и напряженности электростатического поля
 .
.
· Связь между векторами  ,
, 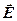 и
и 
 .
.
· Теорема Гаусса для электростатического поля в диэлектрике
 ,
,
где  – алгебраическая сумма заключенных внутри замкнутой поверхности
– алгебраическая сумма заключенных внутри замкнутой поверхности  свободных электрических зарядов;
свободных электрических зарядов;  – составляющая вектора
– составляющая вектора  по направлению нормали
по направлению нормали  к площадке
к площадке  ;
;  – вектор, модуль которого равен
– вектор, модуль которого равен  , а направление совпадает с нормалью
, а направление совпадает с нормалью  к площадке. Интегрирование ведется по всей поверхности.
к площадке. Интегрирование ведется по всей поверхности.
· Электроемкость уединенного проводника и конденсатора
 ,
, 
 ,
,
где  – заряд, сообщенный проводнику;
– заряд, сообщенный проводнику;  – потенциал проводника;
– потенциал проводника;  – разность потенциалов между пластинами конденсатора.
– разность потенциалов между пластинами конденсатора.
· Электроемкость плоского конденсатора
 ,
,
где  – площадь пластины конденсатора;
– площадь пластины конденсатора; 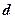 – расстояние между пластинами.
– расстояние между пластинами.
· Электроемкость батареи конденсаторов: при последовательном (а) и параллельном (б) соединениях
а)  , б)
, б)  ,
,
где  – электроемкость
– электроемкость  -го конденсатора;
-го конденсатора;  – число конденсаторов.
– число конденсаторов.
· Энергия уединенного заряженного проводника
 .
.
· Потенциальная энергия системы точечных зарядов
 ,
,
где  – потенциал, создаваемый в той точке, где находится заряд
– потенциал, создаваемый в той точке, где находится заряд  , всеми зарядами, кроме
, всеми зарядами, кроме  -го,
-го,  - число зарядов.
- число зарядов.
· Энергия заряженного конденсатора
 ,
,
где  – заряд конденсатора;
– заряд конденсатора;  – его электроёмкость;
– его электроёмкость;  – разность потенциалов между обкладками.
– разность потенциалов между обкладками.
· Сила притяжения между двумя разноименно заряженными обкладками плоского конденсатора
 .
.
· Энергия электростатического поля плоского конденсатора
 ,
,
где  – площадь одной пластины;
– площадь одной пластины;  – разность потенциалов между пластинами;
– разность потенциалов между пластинами;  – объем области между пластинами конденсатора.
– объем области между пластинами конденсатора.
· Объемная плотность энергии электростатического поля
 ,
,
где  – напряжённость поля,
– напряжённость поля,  – электрическое смещение.
– электрическое смещение.