Между средними величинами

 

В исследованиях часто необходимо сравнение средних арифметических двух групп животных (например, средний вес животных опытной и контрольной групп, среднюю продуктивность дочерей двух производителей). Средние разных групп, как правило, отличаются друг от друга и имеют ошибки, возникающие в результате случайной выборки. Поэтому важно установить достоверна ли разность между средними. С этой целью:

1.Определяется разность (D) между средними арифметическими сравниваемых групп:

где D – разность,

и – средние арифметические сравниваемых групп.

2. Вычисляется ошибка выборочной разности ( ) по формуле:

где и – квадраты ошибок средних арифметических.

3. Определяется критерий достоверности разности ( ) по формуле:

Величина дает возможность оценить достоверность разности.

Известно, что две средние арифметические, полученные в результате случайной выборки из одной совокупности, не могут отличаться друг от друга более чем на три ошибки. Следовательно, если разница превышает тройную ошибку (D > 3 ), то такие средние относятся к разным статистическим совокупностям и можно делать вывод, что разница между группами достоверна, в противном случае существенной разницы нет. Чем выше требования к вероятности вывода, тем шире должен быть интервал, который может обеспечить достоверность. Уровень этой вероятности принято называть достоверностью или надежностью.

В настоящее время применяются три степени вероятности того, что заключение о границах, вмещающих все распределения, будет достоверным: 1 уровень – 95%, 2 уровень – 99%, 3 уровень – 99,9%.

При использовании критерия достоверности возможны два основных случая: – полученный в исследовании критерий достоверности равен или превышает стандартное значение критерия, найденного по Стьюденту – разность достоверна;

– полученный в исследовании критерий достоверности разности меньше стандартного значения для минимального или требуемого порога вероятности – разность недостоверна.

Обычно показатель вероятности обозначается через Р. При указании уровня вероятности пишут: Р 0,95; Р 0,99; Р 0,999 или Р 0,05; Р 0,01; Р 0,001. При использовании таблицы Стьюдента (табл. 1) находят соответствующие значения критерия в этой строчке, которая соответствует числу степеней свободы (V). Число степеней свободы определяется по формуле:

- 2.

Табл. 1 Значение критерия (t) для трех степеней вероятности(Р 0,95), (Р 0,99), (Р 0,999) при числе степеней свободы V (по Стьюденту).

 

V	0,95	0,99	0,999	V	0,95	0,99	0,999
	12,7	63,7	637,0		2,2	3,0	4,1
	4,3	9,9	31,6	14-15	2,1	3,0	4,1
	3,2	5,8	12,9	16-17	2,1	2,9	4,0
	2,8	4,6	8,6	18-20	2,1	2,9	3,9
	2,6	4,0	6,9	21-24	2,1	2,8	3,8
	2,4	3,7	6,0	24-28	2,1	2,8	3,7
	2,4	3,5	5,3	29-30	2,0	2,8	3,7
	2,3	3,4	5,0	31-34	2,0	2,7	3,7
	2,3	3,3	4,8	35-42	2,0	2,7	3,6
	2,2	3,2	4,6	43-62	2,0	2,7	3,5
	2,2	3,1	4,4	63-175	2,0	2,6	3,4
	2,2	3,1	4,3	176 и >	2,0	2,6	3,3

 

Пример № 5. В различных условиях кормления и содержания живая масса бычков симментальской породы составила: в первой группе ( = 25, = 360 ± 9, во второй группе ( = 30, = 320 ± 6.

= 360 – 320 = 40 кг.

Вычисляя td по формуле получим:

Значение вероятности, соответствующее найденному , определяем по таблице Стьюдента, для этого устанавливаем число степеней свободы ( 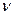). В нашем примере

= 25 + 30 – 2 = 53.

Находим в таблице строку 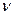= 53, выбираем число равное или превышающее установленное в нашем опыте ( =3,7). Такое число стоит в последней графе ( ). Верхняя строка этой графы показывает искомую вероятность Р > 0,999.

Вывод: разность в живой массе бычков симментальской и холмогорской породы можно считать высоко достоверной при третьем пороге достоверности Р > 0,999.

Задание № 4. По приведенным данным продуктивности чистопородных и помесных коров черно-пестрой породы вычислить , , 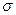и ошибки репрезентативности. Определить достоверность разности продуктивности между чистопородными и помесными животными. Удой коров за 305 дней лактации (кг) (Таблица 2).

Таблица 2

Чистопородные	Помесные

 

Задание № 5. При проведении породоиспытаний (n = 20) в каждой группе в одинаковых условиях кормления и содержания были получены следующие данные продуктивности коров первотелок (Таблица 3).

Таблица 3.

Сведения о продуктивности.

Порода	Удой, кг	Жир, %	Живая масса, кг	Скорость молокоотдачи, кг/мин
Черно-пестрая	3220±50	3,74±0,08	451±15	1,82±0,14
Холмогорская	3150±43	3,65±0,04	439±13	1,75±0,10
Симментальская	2690±31	3,60±0,02	463±12	1,33±0,18
Швицкая	2430±46	3,63±0,06	446±8	1,28±0,1

 

Определить достоверность разности в хозяйственно-полезных качествах данных пород.

 

Контрольные вопросы:

 

1. Что такое ошибка репрезентативности и как она возникает?

2. Как вычисляются ошибки для , , ?

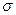3. Отчего зависит величина ошибки репрезентативности?

4. Как определяется достоверность разности?

5. Что значит 1, 2, 3 уровень достоверности (вероятности) ?

6. Как определить степень достоверности по таблице Стьюдента? Приведите примеры.