Тяжести тел. Центры тяжести простейших однородных тел

(треугольника, дуги окружности, дуги окружности, кругового сектора)

 

Цель лекции: Дать определение центру системы параллельных сил и привести формулы для нахождения его координат. Показать пути применения этих формул для определения центра тяжести твердого тела. Вывести формулы координат центра тяжести однородных тел. Указать способы определения центра тяжести и применить их к решениям конкретных задач. Дать учебно-методические рекомендации.

Центр системы параллельных сил

Рассмотрим частный случай пространственной системы сил - параллельные силы. Выберем ось Z параллельно силам. Тогда главный вектор и главный момент принимают вид:

R_x=0 M_OX = åm_x( )

R_y=0 M_OY = åm_y( )

R_z=åF_kz M_OZ = 0

 

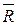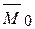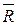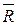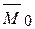Отсюда видно, что главный вектор R расположен по оси Z, а главный момент лежит в плоскости ХОУ. Следовательно, ^ , а потому пространственная система параллельных сил никогда не приводится к динамическому винту. Она приводится к равнодействующей, если ¹ 0 или к паре сил, если =0, или взаимно уравновешивается, если =0, =0.

Рассмотрим систему параллельных сил, которые приводятся к равнодействующей. Вначале рассмотрим две параллельные силы, приложенные в точках А₁ и А₂ и направленные в одну сторону (рис.8.1.).

 

Рис.8.1.

Как известно, их равнодействующая равна = 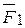+ , направлена в ту же сторону и приложена в точке С, которая делит отрезок А₁А₂ на части, обратно пропорциональные силам:

Повернем теперь силы и вокруг точек их приложения на один и тот же угол в одну и ту же сторону, не изменяя их величин. Получим силы и . Их равнодействующая равна R^*¢= =F₁+F₂, будет параллельна силам и и пройдет опять через точку С, те. она повернется на тот же угол. Очевидно, что этот результат будет справедлив для любой системы параллельных сил.

Точка С, через которую проходит равнодействующая системы параллельных сил при любых поворотах этих сил около точек их приложения в одну и ту же сторону на один и тот же угол, называется центром параллельных сил.

Определим координаты этого центра.

 

Рис.8.2.

 

Пусть имеем систему параллельных сил 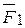, ,…, , 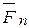приложенных в точках А₁…А_n, положение которых определяется радиусами-векторами (рис.8.2.). Пусть точка С-центр этой системы. Введем единичный вектор , параллельный линиям действия сил. Тогда любая сила может быть представлена в виде:

= × , где

= F_k, - если направления и совпадают и

= - F_k, если направления и противоположны.

Воспользуемся теоремой Вариньона

=å

 

или

х å =å( х )

å х х = å( х х )

 

Перенесем все члены уравнения в одну сторону и вынесем за скобку

(å х - å х ) х = 0

Это векторное произведение равно нулю при любом , т.е. при любом направлении параллельных сил. Коллинеарность векторов исключается, т.к. первый вектор имеем строго определенное направление, а второй вектор -любое. Кроме того ¹0, поэтому

å × - å × =0

Отсюда

= (8.1)

Проектируя обе части равенстве (8.1.) на оси координат, получим формулы для координат центра системы параллельных сил.

X_C= ; Y_C= ; Z_C= (8.2.)

где -алгебраическое значение сил F_k.