Равновесие тела при наличии трения
Многие задачи на равновесие тела при наличии трения удобно решать геометрически, используя конус трения.
Равнодействующая активных сил при равновесии тела (рис.6.3) уравновешивается реакцией  шероховатой поверхности и, следовательно, проходит через вершины конуса на основании аксиомы 2.
шероховатой поверхности и, следовательно, проходит через вершины конуса на основании аксиомы 2.
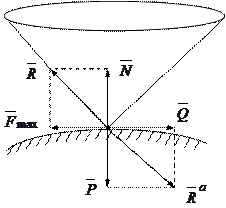 |
Рис.6.3.
Рассмотрим предельный случай равновесия, когда  =
= 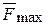 . В этом случае
. В этом случае 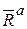 направлена по образующей конуса. Разложим ее на 2 составляющие: 1)силу нормального давления
направлена по образующей конуса. Разложим ее на 2 составляющие: 1)силу нормального давления 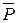 и 2)силу
и 2)силу  , которая стремится заставить тело скользить по поверхности. Очевидно, тело будет находиться в равновесии, пока Q£Fmax, т.е. пока линия действия
, которая стремится заставить тело скользить по поверхности. Очевидно, тело будет находиться в равновесии, пока Q£Fmax, т.е. пока линия действия  будет проходить внутри конуса.
будет проходить внутри конуса.
Итак, имеем следующее геометрическое условие равновесия тела при наличии трения:
Если равнодействующая  всех активных сил, приложенных к телу, проходит внутри конуса трения или по его образующей, то тело находится в равновесии (рис.6.4.).
всех активных сил, приложенных к телу, проходит внутри конуса трения или по его образующей, то тело находится в равновесии (рис.6.4.).
Аналитический метод решения задач статики при наличии трения остается таким же, как и в тех случаях, когда мы трением пренебрегаем. Различие состоит в том, что в уравнениях равновесия учитывается и сила трения, причем обычно рассматривается предельное положение равновесия, когда сила трения достигает своего максимального значения и определяется по формуле Fmax=f×N. Затем составляются обычные уравнения статики, из которых определяются неизвестные величины.
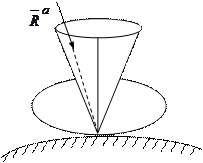 |
Рис.6.4.
Трение качения
Сопротивление, возникающее при качении одного тела по поверхности другого, называется трением качения.
Пусть имеем круглый цилиндрический каток радиуса R и веса P, лежащий на горизонтальной шероховатой плоскости (рис.6.5.).
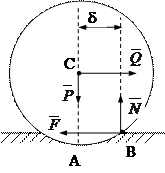 |
Рис.6.5.
К оси катка приложим горизонтальную силу 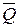 . Вследствие деформации тел их касание происходит не в одной точке, а вдоль некоторой площадки АВ. Под действием силы
. Вследствие деформации тел их касание происходит не в одной точке, а вдоль некоторой площадки АВ. Под действием силы  интенсивность давления у точки А убывает, а у точки В возрастает. В результате этого реакции
интенсивность давления у точки А убывает, а у точки В возрастает. В результате этого реакции  оказывается смещенной в точку В на некоторое расстояние d. В точке В в направлении, обратном направлению
оказывается смещенной в точку В на некоторое расстояние d. В точке В в направлении, обратном направлению 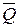 , возникает сила
, возникает сила  , которую называют силой трения качения. Во время равновесия эта сила по модулю равна Q и составляет с ней пару сил (
, которую называют силой трения качения. Во время равновесия эта сила по модулю равна Q и составляет с ней пару сил ( 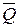 ,
,  ), с моментом Q×R, уравновешиваемую парой (
), с моментом Q×R, уравновешиваемую парой ( 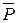 ,
, 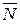 ) , момент которой называется моментом трения качения и который численно равен M=N×d.
) , момент которой называется моментом трения качения и который численно равен M=N×d.
Здесь d называется коэффициентом трения качения. Он имеет размерность длины и определяется опытным путем. Коэффициент трения качения зависит от материала тел и физического состояния их поверхности.
Из равенства моментов уравновешиваемых пар имеем:
Q×R= N×d.
Отсюда
Q=  .
.
Отношение 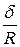 для большинства материалов значительно меньше статического коэффициента трения скольжения f.
для большинства материалов значительно меньше статического коэффициента трения скольжения f.
Этим объясняется, что в технике, когда это возможно, стремятся заменить скольжение качением (колеса, подшипники и др.).
Вопросы для самопроверки
1. Что называется трением скольжения?
2.Сформулируйте законы трения скольжения.
3.Что называется углом трения? Как связан угол трения с коэффициентом трения?
4.От чего зависит коэффициент трения скольжения при покое и при движении?
5.Что представляет собой конус трения?
6.Сформулируйте геометрическое условие равновесия тела при наличии трения.
7.Чем отличается аналитические уравнения равновесия тела, находящегося на шероховатой поверхности от обычных уравнений равновесия?
8.Что называется трением качения?
9.Объясните причины, вследствие которых возникает сопротивление качению одного тела на поверхность другого.
10.Что представляет собой коэффициент трения качения? Какова его размерность? От чего он зависит?
ЗАДАЧИ
1)Найти наибольший угол a, при котором тело М не будет соскальзывать со сферической поверхности, если коэффициент трения скольжения равен f. Размерами тела пренебречь.
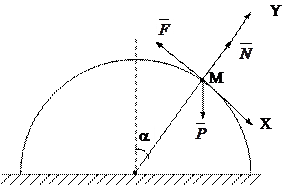 |
Решение. Рассмотрим предельное положение равновесия, при котором сила трения равна
F=f×N.
При этом на тело будет действовать сходящаяся плоская система сил 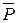 ,
,  ,
, 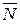 (
( 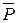 -вес тела,
-вес тела, 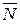 -нормальная реакция поверхности,
-нормальная реакция поверхности,  -сила трения).
-сила трения).
Составим уравнения равновесия:
åFkx=0 P×sina-F=0 (1)
åFky=0 N-P×cosa=0 (2)
Из (2) имеем N= P×cosa. Тогда F=f×N=f×P×cosa.
Подставим в (1)
P×sina - f×P×cosa =0
tga=f
Отсюда
a=arctg f.
2)При каком минимальном коэффициенте трения между полом и лестницей последняя может находиться в равновесии, опираясь верхним концом о гладкую стену? Вес лестницы G=120 Н. Угол наклона лестницы в вертикальной стене a=300.
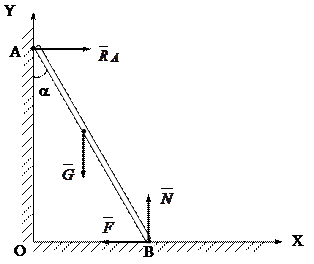 |
Решение: На лестницу действует активная сила 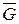 , реакция гладкой стены
, реакция гладкой стены  и реакция шероховатого пола, которую разложим на 2 составляющие:
и реакция шероховатого пола, которую разложим на 2 составляющие:
1. 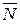 -нормальная составляющая,
-нормальная составляющая,
2. F-сила трения, причем принимаем, что F=f×N.
Имеем плоскую систему сил. Составим три уравнения равновесия:
åFkx=0 RA-F=0
åFky=0 N-G=0
åmB(  )=0 G×
)=0 G× 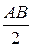 ×sina-RA×AB×cosa=0
×sina-RA×AB×cosa=0
Отсюда
F=RA= 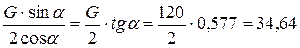 Н.
Н.
N=G=120 H.
Тогда
f=  =0,29.
=0,29.
3)К вертикальной стене представлена лестница АВ, опирающаяся своим нижним концом на горизонтальный пол. Коэффициент трения лестницы о стенку f1, о пол-f2. Вес лестницы вместе с находящимся на ней человеком равен Р и приложен в точке С, которая делит длину лестницы в отношении m/n. Определить наибольший угол a, составляемый лестницей со стеной в положении равновесия, а также нормальные составляющие реакций NA стены и NB пола для этого значения a.
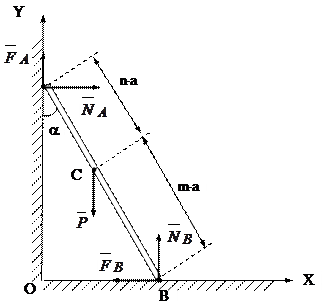 |
Решение: На лестницу действует активная сила 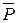 и реакция шероховатых стены и пола, которые разложим соответственно на составляющие
и реакция шероховатых стены и пола, которые разложим соответственно на составляющие 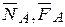 и
и 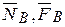 . Будем рассматривать предельное положение равновесия лестницы. Тогда
. Будем рассматривать предельное положение равновесия лестницы. Тогда
FA=f1×NA, FB=f2×NB.
Составим три уравнения равновесия:
åFkx=0 NA-FB=0 (1)
åFky=0 FA-P+NB=0 (2)
åmB(  )=0 P×m×a×sina+NA(m+n)a×cosa-FA(m+n) a×sina=0 (3)
)=0 P×m×a×sina+NA(m+n)a×cosa-FA(m+n) a×sina=0 (3)
Из (1) находим NA=FB=f2NB. Подставим в (2)
f1× f2×NB-P+NB=0
NB(f1× f2+1)=P
Тогда
NB= 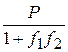 ,
,
N2= 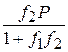 .
.
Из уравнения (3) определяем неизвестный угол a, предварительно разделив почленно на cosa.
Pmtga-NA(m+n)-FA(m+n)tga=0
tga[Pm-NAf1(m+n)]=NA(m+n)
tga= 
= 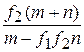 .
.