Эквивалентности пары сил. Условие равновесия пар сил
В начале ответим на вопрос имеют ли равнодействующую две равные антипараллельные силы, т.е. противоположно направленные силы? Для ответа на этот вопрос, проанализируем изменение модуля равнодействующей и положение центра С антипараллельных сил, когда сила  по модулю стремится к силе
по модулю стремится к силе  .
.
Как известно, вектор равнодействующей  двух неодинаковых по модулю антипараллельных сил
двух неодинаковых по модулю антипараллельных сил  и
и  определяется по формуле
определяется по формуле  =
=  -
-  . Если значение модуля с одной из этих сил
. Если значение модуля с одной из этих сил  будет стремиться к значению модуля другой F2, т.е. F1®F2, то в пределе R=F1=F2=0. Расстояние АС до точки приложения равнодействующей
будет стремиться к значению модуля другой F2, т.е. F1®F2, то в пределе R=F1=F2=0. Расстояние АС до точки приложения равнодействующей 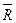 , согласно формуле (3.3) стремится к бесконечности при F1®F2. Следовательно, если в различных точках тела действует система двух равных, но противоположно направленных сил, то она не имеет равнодействующую и эту систему нельзя ни заменить, ни уравновесить одной силой, т.е. этот случай представляет пример совокупности сил, не находящихся в равновесии и не имеющих равнодействующей. Система таких сил обычно стремится произвести вращение твердого тела, к которому она приложена. Понятие о них как о паре сил впервые в науку было введено французским ученым Пуансо.
, согласно формуле (3.3) стремится к бесконечности при F1®F2. Следовательно, если в различных точках тела действует система двух равных, но противоположно направленных сил, то она не имеет равнодействующую и эту систему нельзя ни заменить, ни уравновесить одной силой, т.е. этот случай представляет пример совокупности сил, не находящихся в равновесии и не имеющих равнодействующей. Система таких сил обычно стремится произвести вращение твердого тела, к которому она приложена. Понятие о них как о паре сил впервые в науку было введено французским ученым Пуансо.
Итак, система двух равных по величине, параллельных и противоположно направленных сил  и
и  , приложенных в различные точки твердого тела называется парой сил. Она обозначается (
, приложенных в различные точки твердого тела называется парой сил. Она обозначается (  ,
,  ). Причем наикратчайшее расстояние между линиями действия сил, составляющих пару, называется плечом пары. Обозначим его через букву d.
). Причем наикратчайшее расстояние между линиями действия сил, составляющих пару, называется плечом пары. Обозначим его через букву d.
Действие пары сил, оказываемое на твердое тело обычно характеризуется ее моментом, обозначаемым m(  ,
,  ). Алгебраический момент пары сил находится как произведение модуля одной из сил пары на ее плечо, взятое со знаком ±
). Алгебраический момент пары сил находится как произведение модуля одной из сил пары на ее плечо, взятое со знаком ±
m(  ,
,  )=±F×d (3.4)
)=±F×d (3.4)
При этом, если пара сил стремится вращать тело против движения часовой стрелки, то ее момент считается положительным, в обратном случае отрицательным.
Размерность пары сил зависит от размерностей силы и расстояния между линиями действия сил. Если силы измерять ньютонами (Н), а плечо метрами (М), то момент пары сил будет измеряться ньютонметрами (Н.М.).
Кроме числовой величины F×d момент пары сил зависит еще и от того, как расположена плоскость действия пары в пространстве. Следовательно, момент пары сил есть величина векторная. В целом его можно сформулировать следующим образом: момент пары сил есть вектор, перпендикулярный к плоскости действия пары, направленный по правилу правого винта и численно равный произведению одной из сил пары на плечо. Таким образом, доказано, что пара сил сообщает телу вращательное движение, причем вращательный эффект пары тем больше, чем больше модули сил у пары и ее плечо. Вращательный эффект действия пары измеряют величиной называемой моментом пары сил. В случае пространственной системы пар для полной характеристики вращательного действия пары сил на тело надо еще указать и направление в пространстве плоскости действия. Момент пары будет изображаться вектором, перпендикулярным к этой плоскости. Теперь необходимо выяснить точку приложения этого вектора. Для этого рассмотрим несколько теорем об эквивалентности пар, из которых следует, что вектор-момент пары может быть приложен в любой точке пространства, т.е. он является свободным.
Теорема 1. Любую пару сил, действующую на твердое тело, не нарушая его прежнего состояния, можно перенести в любое положение в ее плоскости действия.
Пусть на тело в точках А и В приложены силы  ,
,  , которые составляют пару сил (рис.3.3).
, которые составляют пару сил (рис.3.3).
 |
Рис.3.3.
Далее возьмем произвольно расположенный отрезок (CD) по длине равный плечу h данной пары (  ,
,  ) и покажем, что не нарушая равновесия тела, можно эту пару перенести так, чтобы ее плечо совпало с отрезком CD. Для этого проведем линии действия z1 и z2 сил
) и покажем, что не нарушая равновесия тела, можно эту пару перенести так, чтобы ее плечо совпало с отрезком CD. Для этого проведем линии действия z1 и z2 сил  и
и  и восстановим в точках С и D перпендикуляры z3 и z4 к отрезку CD. При этом точки пересечения прямых z1 и z3, а также z2 и z4 соответственно отметим через буквы M и N. Так как силы F1 и F2 есть скользящие вектора, то их перенесем в эти точки. Затем к этим точкам приложим взаимно уравновешивающихся силы
и восстановим в точках С и D перпендикуляры z3 и z4 к отрезку CD. При этом точки пересечения прямых z1 и z3, а также z2 и z4 соответственно отметим через буквы M и N. Так как силы F1 и F2 есть скользящие вектора, то их перенесем в эти точки. Затем к этим точкам приложим взаимно уравновешивающихся силы  ,
,  и
и  ,
,  численно равные силам
численно равные силам  и
и  и направленные соответственно по прямым z3 и z4.
и направленные соответственно по прямым z3 и z4.
Согласно аксиомы 4, построив на силах  ,
,  и
и  ,
,  параллелограммы, получим их равнодействующие
параллелограммы, получим их равнодействующие  и
и  . Однако эти параллелограммы равны между собой, следовательно
. Однако эти параллелограммы равны между собой, следовательно  =-
=-  , R1=R2. Кроме того вектор
, R1=R2. Кроме того вектор  делит пополам угол между векторами
делит пополам угол между векторами  и
и  , но прямая MN также делит его на пополам. Следовательно
, но прямая MN также делит его на пополам. Следовательно  направлен по MN. Аналогичным образом доказываем, что
направлен по MN. Аналогичным образом доказываем, что  также направлен по MN. Значит силы
также направлен по MN. Значит силы  и
и  равны по величине и действуют по одной прямой MN в противоположные стороны, т.е. они взаимно уравновешиваются. Теперь оставшиеся силы
равны по величине и действуют по одной прямой MN в противоположные стороны, т.е. они взаимно уравновешиваются. Теперь оставшиеся силы  =
=  и
и  =
=  перенесем в точки С и D соответственно по прямым z3 и z4.
перенесем в точки С и D соответственно по прямым z3 и z4.
Таким образом, пара, действующая на тело из одного положения, перенесена в требуемое значение.
Теорема 2. Действие пары сил, оказываемое на тело не изменится от переноса параллельно самой себе ее плоскости действия.
Пусть на тело приложена пара сил (  ,
,  ) с плечом АВ (рис.3.4).
) с плечом АВ (рис.3.4).
 |
Рис.3.4.
Переносив это плечо параллельно самому себе в положение CD, приложим к точкам С и D соответственно силы  ,
,  и
и  ,
,  по величине равные силам пары (
по величине равные силам пары (  ,
,  ) и направленные параллельно им. Тогда система сил (
) и направленные параллельно им. Тогда система сил (  ,
,  )~(
)~(  ,
,  ,
,  ,
,  ,
,  ,
,  ). Далее сложив силы F1 и S1, равные по величине 2F и взаимно противоположно направленные
). Далее сложив силы F1 и S1, равные по величине 2F и взаимно противоположно направленные  и
и  получим две силы, приложенные в середине диагонали параллелограмма ABCD. Следовательно эти две силы взаимно уравновешиваются. Отсюда вытекает, что система (
получим две силы, приложенные в середине диагонали параллелограмма ABCD. Следовательно эти две силы взаимно уравновешиваются. Отсюда вытекает, что система (  ,
,  ,
,  ,
,  ) или (
) или (  ,
,  ,
,  ,
,  ,
,  ,
,  )~(
)~(  ,
,  ), т.е. оставшаяся пара (
), т.е. оставшаяся пара (  ,
,  ) эквивалентна в начале действующей на тело паре (
) эквивалентна в начале действующей на тело паре (  ,
,  ).
).
Таким образом, приходим к выводу, что плоскость любой пары сил действительно можно переносить параллельно самой себе, не изменяя при этом действия, оказываемого на тело.
Теорема 3. Действие пары сил, оказываемое на тело не изменится, если момент пары всегда остается постоянным при изменении ее плеча силы.
Для доказательства этой теоремы допустим, что на какое-то абсолютно твердое тело действует пара сил (  ,
,  ) (рис.3.5). Силу
) (рис.3.5). Силу  , приложенную в точку А, согласно сложения двух параллельных сил, направленных в одну сторону, разложим на две составляющие
, приложенную в точку А, согласно сложения двух параллельных сил, направленных в одну сторону, разложим на две составляющие  и
и  -
-  , приложенные в точках С и В. Тогда силы
, приложенные в точках С и В. Тогда силы  и (
и (  -
-  ), приложенные в точку В имеет равнодействующую
), приложенные в точку В имеет равнодействующую  , численное значение которой равно S2=F2-(F1-S1)=S1. В результате находим новую пару
, численное значение которой равно S2=F2-(F1-S1)=S1. В результате находим новую пару  ,
,  , плечо которой равно СВ. Однако для этой пары сила S1 и плечо СВ удовлетворяют соотношению
, плечо которой равно СВ. Однако для этой пары сила S1 и плечо СВ удовлетворяют соотношению  или S1(CB)=F1(AB). Здесь произведения S1×(CB) и F1×(AB) соответственно являются моментами пар сил (
или S1(CB)=F1(AB). Здесь произведения S1×(CB) и F1×(AB) соответственно являются моментами пар сил (  ,
,  ) и (
) и (  ,
,  ), что и доказывает данную теорему.
), что и доказывает данную теорему.
 |
Рис.3.5.
Из рассмотренных теорем следует, что а)вектор-момент пары является свободным вектором и он может быть переведен в любую точку пространства, б)пары, имеющие равные векторы-моменты, эквивалентны, с)не изменяя численное значение момента и направления вращения пары сил можно изменять ее модуль и плечо. Следовательно, основной характеристикой пары сил является ее вектор-момент, так как он полностью определяет все необходимые ее элементы, т.е. положение плоскости действия пары сил, направление вращения и числовое значение момента.
Теперь докажем следующую теорему о сложении пар и определим такие условия, при которых система пар сил, действующих на тело находилась в состоянии равновесия.
Теорема 4. Система пар сил, как угодно расположенных в пространстве всегда эквивалентна одной паре, момент которой равен геометрической сумме моментов слагаемых пар.
Для доказательства этой теоремы, в начале рассмотрим сложение двух пар сил (  ,
,  ) и (
) и (  ,
,  ), расположенных в пересекающихся плоскостях П1 и П2 (рис.3.6) (обе пары в своих плоскостях могут быть ориентированы любым образом). Выбрав на линии пересечения плоскостей некоторый отрезок AB=d, согласно теоремы 3, приведем к нему обе пары, конечно изменив при этом численные значения сил, составляющих пары.
), расположенных в пересекающихся плоскостях П1 и П2 (рис.3.6) (обе пары в своих плоскостях могут быть ориентированы любым образом). Выбрав на линии пересечения плоскостей некоторый отрезок AB=d, согласно теоремы 3, приведем к нему обе пары, конечно изменив при этом численные значения сил, составляющих пары.
 |
Рис.3.6.
При этом вместо пар (  ,
,  ) и (
) и (  ,
,  ) получим эквивалентные им пары (
) получим эквивалентные им пары (  ,
,  ) и (
) и (  ,
,  ), лежащих в тех же П1 и П2 плоскостях. Здесь (
), лежащих в тех же П1 и П2 плоскостях. Здесь (  ,
,  )~(
)~(  ,
,  ), (
), (  ,
,  )~(
)~(  ,
,  ).
).
Следовательно, m  =m(
=m(  ) и m(
) и m(  )=m(
)=m(  ) |m(
) |m(  )|=F1d; |m(
)|=F1d; |m(  )|=S1d. Кроме того прямая АВ перпендикулярна к линиям действия сил
)|=S1d. Кроме того прямая АВ перпендикулярна к линиям действия сил  ,
,  и
и  ,
,  , так как отрезок d является плечом обеих пар. Далее складывая попарно силы
, так как отрезок d является плечом обеих пар. Далее складывая попарно силы  ,
,  и
и  ,
,  , находим новую пару (
, находим новую пару (  ,
,  ). Она эквивалентна системе двух пар, приложенных к телу. Теперь определим момент пары
). Она эквивалентна системе двух пар, приложенных к телу. Теперь определим момент пары  ,
,  . На основании данного определения для момента пары имеем, что m(
. На основании данного определения для момента пары имеем, что m(  )=
)=  х
х  . Однако
. Однако  =
= 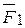 +
+  и, следовательно,
и, следовательно,
m(  )=
)=  х(
х( 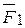 +
+  )=
)=  х
х 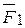 +
+  х
х  = m(
= m(  )+m(
)+m(  )
)
или
 .
.
Последнее выражение дает доказательство теоремы о сложении пар. Далее использовав эту теорему, любую систему пар можно привести к простейшему виду. Действительно, если дана система пар (  ,
,  ), (
), (  ,
,  ),…(
),…(  ) как угодно расположенных в пространстве, моменты которых
) как угодно расположенных в пространстве, моменты которых  , на основании последней теоремы, первые две пары можно заменить одной парой (
, на основании последней теоремы, первые две пары можно заменить одной парой (  ) с моментом
) с моментом
 =
=  +
+ 
Полученную пару (  ,
,  ) сложим с парой (
) сложим с парой (  ), тогда получим новую пару
), тогда получим новую пару  ,
,  с моментом
с моментом  =
=  +
+  =
=  +
+  +
+  . Продолжая эту процедуру и дальше, наконец находим последнюю результирующую пару
. Продолжая эту процедуру и дальше, наконец находим последнюю результирующую пару  с моментом
с моментом
 =
=  +
+  +…+
+…+  =
=  (3.5)
(3.5)
Таким образом, любая система пар, действующая на абсолютно твердое тело приводится к одной паре (3.5), момент которой равен геометрической сумме моментов данных пар и тело под действием такой пары, естественно, будет находиться в состоянии равновесия только тогда, когда ее момент равен нулю, т.е. система пар сил взаимно уравновешивается
 =0 или
=0 или  = 0 (3.6)
= 0 (3.6)
Следовательно, условие равновесия пар сил, произвольно расположенных в пространстве, можно сформулировать следующим образом:
Система пар сил, расположенных как угодно в пространстве, находится в равновесии, если геометрическая сумма моментов всех сил будет равна нулю.
Выражение (3.6) в координатной форме записывается следующим образом:
 ,
,  ,
,  . (3.7)
. (3.7)