Совокупность

Характеристики выборки могут быть распространены на генеральную совокупность с помощью одного из двух способов распространения выборочных данных:

- способа прямого пересчета;

- способа поправочных коэффициентов.

При первом способе средние величины и доли, полученные по выборке, переносятся на генеральную совокупность. При этом генеральная средняя определяется как , а генеральная доля – как Р .

Способ поправочных коэффициентов применяется, когда целью выборочного исследования является уточнение результатов сплошного наблюдения. Для этого после обобщения данных сплошного наблюдения практикуется 10%-ное выборочное наблюдение с установлением поправочного коэффициента , который устанавливает процент расхождений между данными сплошного и выборочного наблюдения.

Например, при проведении сплошного учета уличных торговых мест в городе их было зарегистрировано N=1000 шт. С целью уточнения данных через полгода был проведен контрольный обход части города и зарегистрировано 210 уличных торговых мест. По данным сплошного учета их было 200шт.

Необходимо уточнить число уличных торговых мест на новую дату:

На новую дату число торговых мест составят

 

6.8 Проверка статистических гипотез

Статистическая гипотеза – это гипотеза, которая допускает наблюдения статистической природы. Такие наблюдения могут возникать в различных областях деятельности человека. Вот некоторые примеры.

1) Вероятности выпадения каждой грани игральной кости равны. Это означает, что мы имеем равномерное распределение случайной переменной, которая представляет собой число точек на лицевой поверхности каждой грани данной кости.

2) Средняя длина детали, поступившей от нашего поставщика, больше, чем он заявлял (или меньше, или отличается от заявленной).

3) Средняя оценка стандартного тестирования у обучавшихся по новому методу выше, чем у обучавшихся по старому методу.

4) Значения параметров, характеризующих чистоту воздуха в городе, больше, чем установлено стандартом.

5) Для некоторых работодателей переменная "принятие на работу" не будет независимой от переменной "пол" (или "этническая принадлежность", "вероисповедание" и т. д.).

Из приведенных примеров следует, что статистическая гипотеза – это утверждение относительно характера или неизвестных параметров распределения случайных величин.

Гипотеза1 является гипотезой относительно абстрактной модели, вероятностном распределении случайной переменной, которая описывает игральную кость. Данная гипотеза может быть проверена с помощью наблюдений, например, 100 бросаний кости. Следующие три гипотезы касаются параметра. Они проверяются с помощью выборочных данных. Эти данные рассматриваются как выборочное распределение, необходимое для оценки параметра. Последняя гипотеза утверждает независимость двух качественных (нечисловых) переменных. Она проверяется путем сравнения наблюдаемых данных с истинными данными, ожидаемыми в случае независимости переменных. Отметим, что только три из пяти гипотез включает параметр, две другие представляют собой статистически утверждения другого рода.

Для каждого из этих примеров практически невозможно непосредственно определить истинность гипотезы. Например, вероятностное распределение для кости является моделью всех возможных бросаний, которые мы не можем наблюдать. Практически невозможно измерить длину каждой из сотен, а может быть и тысяч поступающих деталей. Для гипотезы (3) невозможно протестировать сегодня всех студентов, которые должны обучаться по новому методу в ближайшие 15 лет. Конечно, можно протестировать студентов через год после окончания обучения. Но оценку эффективности нового метода нужно делать до его реализации, а не после. А для гипотезы (4) можно ли проверить каждый кубический метр воздуха в городе? Наконец, что означает (5) прямая верификация для каждого человека?

Из-за невозможности определить истинность гипотезы прямым путем, мы "проверяем" гипотезу, т.е. устанавливаем, не противоречит ли высказанная нами гипотеза имеющимся выборочным данным. Эта процедура носит название статистической проверки гипотез.

Результат сопоставления высказанной гипотезы с выборочными данными может быть либо отрицательным (данные наблюдения противоречат высказанной гипотезе, а поэтому гипотезу надо отклонить), либо неотрицательным (данные наблюдения не противоречат высказанной гипотезе, а поэтому ее можно принять в качестве одного из возможных решений).

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. Следовательно, эти гипотезы целесообразно различать.

Нулевая гипотеза (H0) – это основное проверяемое предположение, которое обычно формулируется как отсутствие различий, отсутствие влияния фактора, отсутствие эффекта, равенство нулю значений выборочных характеристик и т.п. Примером нулевой гипотезы является утверждение о том, что различие в результатах выполнения двумя группами учащихся одной и той же контрольной работы вызвано лишь случайными причинами.

Другое проверяемое предположение (не всегда строго противоположное или обратное первому) называется конкурирующей или альтернативной гипотезой. Так, для упомянутого выше примера гипотезы Н0 одна из возможных альтернатив Н1 будет определена как: уровни выполнения работы в двух группах учащихся различны и это различие определяется влиянием неслучайных факторов, например, тех или других методов обучения.

С точки зрения статистической проверки гипотез существуют только два вида ошибок, называемые ошибкой I рода и ошибкой II рода.

Ошибка I рода – это неправильное действие в соответствии с Н1: действовать в соответствии с Н1, если справедлива Н0, т.е. ошибочно отвергнуть нулевую гипотезу. Ошибка II рода – это неправильное действие в соответствии с Н0: действовать в соответствии с Н0, если справедлива Н1. Вероятность ошибки интерпретируется как условная вероятность. Условные вероятности этих двух типов ошибок обозначаются соответственно α и β:

α = Р(ошибка I рода) = Р(действие в соответствии с Н1| Н0 истинна);

β = Р(ошибка II рода) = Р(действие в соответствии с Н0| Н1 истинна).

В таблице 6.5 показаны возможности принятия решения и ошибки двух типов по отношению к гипотезе Н0. Отметим, что если гипотеза Н0 справедлива и она принимается, то в таблице указано, что решение принято правильно. Если справедлива гипотеза Н1, а принимается Н0 , то при решении допущена ошибка II рода. Если справедлива гипотеза Н0 , а принимается гипотеза Н1, то при решении допущена ошибка I рода.

 

Таблица 6.5 - Решения и ошибки при статистической проверке гипотез

 

	Состояние реального мира (неизвестное нам)
Н1 ложна (Н0 истинна)	Н1 истинна
Наше решение, основанное на данных	Действие в соответствии с Н0	Правильное решение	Ошибка II рода
Действие в соответствии с Н1	Ошибка I рода	Правильное решение

 

Вероятность появления ошибки I рода называют уровнем значимости. Если уровень значимости равен 5%, это означает, что существует возможность отвергнуть правильную нулевую гипотезу в одном случае из 20. Если уровень значимости равен 1% - то в одном случае из 100.

Существуют два возможных вывода при проверке гипотезы: либо мы отклоняем нулевую гипотезу ("отклонить Н0)", либо мы отказываемся отклонить нулевую гипотезу ("отказ отклонить Н0)". Рассмотрим смысл каждого из этих выводов и соответствующие ошибки на примере, связанном с контролем качества. Пусть р – доля дефектных изделий, выпускаемых производственной линией. Сформулируем две гипотезы:

Н0: р = 0.01; Н1: р > 0.01.

Предполагая 5 %-ный уровень значимости, рассмотрим возможные выводы и их интерпретацию.

Отклонить Н0:Свидетельства предполагают, что контроль качества ослаб, необходимо остановить производство и выполнить корректирующие действия.

Отказ отклонить Н0:Тест не дает выводов, так как отсутствуют свидетельства того, что контроль качества ослаб, производство остается без изменений.

Ошибка I рода:С 5 %-ным риском ошибки мы останавливаем производство без необходимости. Доля дефектных изделий не превышает заданный уровень, даже если мы основываемся на неверных свидетельствах.

Ошибка II рода:Мы продолжаем производство с неизвестным риском ошибки, когда число дефектных изделий среди выпускаемых больше, чем допускают требования контроля качества.

Формальные выводы ведут к реальным действиям. "Отклонить Н0" означает "действовать в соответствии с Н1", "Отказ отклонить Н0" означает "действовать в соответствии с Н0".

Рассмотрим пример проверки гипотезы о среднем значении μ диаметра поставляемых деталей:

Н0: μ = 3.15; Н1: μ < 3.15.

Отклонить Н0:Это означает, детали машины, которые мы получаем от поставщика, имеют недопустимо малый диаметр (среднее значение диаметра меньше, чем 3.15 мм). Ошибка в данном случае составляет 5 %.

Отказ отклонить Н0:Тест не дает выводов. Отсутствуют свидетельства нарушений условий поставки партии деталей, поставляемая партия принимается.

Ошибка I рода:Существует 5 %-ный риск того, что, основываясь на ошибочных свидетельствах, мы отклоним партию деталей, хотя среднее значение диаметра не будет меньше, чем 3.15 мм.

Ошибка II рода:Так как у нас отсутствовали необходимые свидетельства, мы принимаем поставляемую партию деталей, хотя их размеры не соответствуют требованиям.

Статистика критерия (Т) — некоторая функция от исходных данных, по значению которой проверяется нулевая гипотеза. Чаще всего статистика критерия является числовой функцией, но она может быть и любой другой функцией, например, многомерной функцией.

Всякое правило, на основе которого отклоняется или принимается нулевая гипотеза называется критерием для проверки данной гипотезы. Статистический критерий (критерий) – это случайная величина, которая служит для проверки статистических гипотез.

Критическая область – совокупность значений критерия, при котором нулевую гипотезу отвергают. Область принятия нулевой гипотезы (область допустимых значений) – совокупность значений критерия, при котором нулевую гипотезу принимают. При справедливости нулевой гипотезы вероятность того, что статистика критерия попадает в область принятия нулевой гипотезы должна быть равна 1-Ркр.

Процедура проверки нулевой гипотезы в общем случае включает следующие этапы:

1. Задается допустимая вероятность ошибки первого рода (Ркр=0,05)

2. Выбирается статистика критерия (Т)

3. Ищется область допустимых значений

4. По исходным данным вычисляется значение статистики Т

5. Если Т (статистика критерия) принадлежит области принятия нулевой гипотезы, то нулевая гипотеза принимается (корректнее говоря, делается заключение, что исходные данные не противоречат нулевой гипотезе), а в противном случае нулевая гипотеза отвергается и принимается альтернативная гипотеза. Это основной принцип проверки всех статистических гипотез.

В современных статистических пакетах на ЭВМ используются не стандартные уровни значимости, а уровни, подсчитываемые непосредственно в процессе работы с соответствующим статистическим методом. Эти уровни, обозначенные буквой P, могут иметь различное числовое выражение в интервале от 0 до 1, например, 0,7 0,23 0,012. Понятно, что в первых двух случаях полученные уровни значимости слишком велики и говорить о том, что результат значим, нельзя. В последнем случае результаты значимы на уровне 12 тысячных. Это достоверный результат.

При проверке статистических гипотез с помощью статистических пакетов, программа выводит на экран вычисленное значение уровня значимости Р и подсказку о возможности принятия или неприятия нулевой гипотезы.

Если вычисленное значение Р превосходит выбранный уровень Ркр, то принимается нулевая гипотеза, а в противном случае — альтернативная гипотеза. Чем меньше вычисленное значение Р, тем более исходные данные противоречат нулевой гипотезе.

Число степеней свободы у какого-либо параметра определяют как число опытов, по которым рассчитан данный параметр, минус количество одинаковых значений, найденных по этим опытам независимо друг от друга.

Величина Ф называется мощностью критерия и представляет собой вероятность отклонения неверной нулевой гипотезы, то есть вероятность правильного решения. Мощность критерия – вероятность попадания критерия в критическую область при условии, что справедлива альтернативная гипотеза. Чем больше Ф, тем вероятность ошибки II-го рода меньше.

Между уровнем значимости и мощностью критерия имеется определенная связь. Так, с уменьшением уровня значимости падает мощность критерия.

Рассмотрим критерий однородности совокупности, или типичности средней.

Каждый случай исчисления средних величин должен дополняться проверкой однородности совокупности. Это может оказаться необходимым, например, при решении следующих задач:

- изучении ритмичности выпуска продукции;

- анализе сезонности производства;

- оценке мероприятий, направленных на улучшение организации труда и т.д.

При формулировании критериев однородности изучаемой совокупности используют а) коэффициент вариации б) размах вариации.

Например: Имеются данные о выпуске продукции за каждую декаду месяца первых трех месяцев года. В цехе осуществляются организационно-технические мероприятия. Можно ли по приведенным данным судить о том, что проводимые мероприятия ведут к увеличению объема выпуска продукции.

 

Номер декады	Объем выпуска, шт.

Нулевая гипотеза: проводимые мероприятия ведут к увеличению объема выпускаемой продукции. Гипотеза будет принята, если значение коэффициента вариации превысит критическое значение – 35%.

Среднее значение выпуска продукции равно 117 штук. Среднее квадратическое отклонение 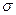=20,64, а коэффициент вариации 0,176 или 17,6%. В данном случае, фактическое значение коэффициента вариации ниже критического. Следовательно можно считать, что изменчивость показателей выпуска продукции лежит в пределах случайных колебаний и не связана с проводимыми мероприятиями. Иными словами, приведенные данные о выпуске продукции не являются достаточным основанием для вывода о постоянно действующей закономерности. Нулевая гипотеза отвергается.