Контрольная работа №6
441 - 450. Методом Даламбера найти уравнение и = и(х, t) формы однородной бесконечной струны, определяемой волновым уравнением 
, если в начальный момент tо = 0 форма струны и скорость точки струны с абсциссой х определяются соответственно заданными функциям 
441. f(x)=x(2-x), F(x)=e-x.
442. f(x)=x2, F(x)= sin x.
443. f(x)=ex, F(x)=ωx.
444. f(x)=cos x, F(x)=ωx.
445. f(x)=sin x, F(x)=υ0.
446. f(x)=x, F(x)= cos x.
447. f(x)= sin x, F(x)= cos x.
448. f(x)=x(x-2), F(x)= ex .
449. f(x)= cos x, F(x)= υ0.
450. f(x)=e-x, F(x)= sin x.
451-460.Методом Фурье найти решение 
уравнения теплопроводности 
, если в начальный момент времени 
температура стержня длины 
определяется заданной функцией 
, а на границах стержня температура задается постоянной и равной, т.е. 
.
451. f(x)=x
452.f(x)=1
453.f(x)=x-1
454.f(x)=x+1
455.f(x)=2x-1
456.f(x)=2x+1
457.f(x)=1-3x
458.f(x)= 
459.f(x)= 
460.f(x)=1-2x
461 - 470. Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
461. 
, 
462. 
, 
463. 
, 
464. 
,
465. 
, 
466. 
, 
467. 
, 
468. 
,
469. 
,
470. 
, 
471 - 480. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее начальным условиям.
471. 
x(0)=1, y(0)=0.
472. 
x(0)=1, y(0)=1, z(0)=1.
473. 
x(0)=2, y(0)=3.
474. 
x(0)=2, y(0)=1/2, z(0)=5/2.
475. 
x(0)=1, y(0)=1.
476. 
x(0)=2, y(0)=2, z(0)=-1.
477. 
x(0)=0, y(0)=0.
478. 
x(0)=1, y(0)=2, z(0)=3.
479. 
x(0)=1, y(0)=-1.
480. 
x(0)=1, y(0)=1.
481. Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что: а) студент знает все три вопроса; б) только два вопроса; в) только один вопрос экзаменационного билета.
482. В каждой из двух урн находятся 5 белых и 10 черных шаров. Из первой урны во вторую переложили неудачу один шар, а затем из второй урны вынули наугад один шар. Найти вероятность того, что вынутый шар окажется черным.
483. Три стрелка в одинаковых и независимых условиях производили по одному выстрелу по одной и той же целию Вероятность поражения цели первым стрелком равна 0,9, вторым – 0,8, третьим – 0,7. Найти вероятность того, что: а) только один из стрелков попадает в цель; б) только два стрелка попадут в цель; в) все три стрелка попадут в цель.
484. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 1600 испытаниях событие наступит 1200 раз.
485. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равна 0,9, второе – 0,95, третье – 0,85. Найти вероятность того, что при аварии сработает: а) только одно устойство; б) только два устройства; в) все три устройства.
486. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,02. Найти вероятность того, что в 150 испытаниях событие наступит 5 раз.
487. В партии из 1000 изделий имеются 10 дефектных. Найти вероятность того, что среди 50 изделий, наудачу взятых из этой партии, ровно три окажутся дефектными.
488. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 125 испытаниях событие наступит не менее 75 и не более 90 раз.
489. На трех станках при одинаковых и независимых условиях изготовляют детали одного наименования. На первом станке изготовляют 10%, на втором – 30, на третьем – 60% всех деталей. Вероятность каждой детали быть бездефектной равна 0,7, если она изготовлена на первом станке, 0,8, - если на втором станке, и 0,9, - если на третьем станке. Найти вероятность того, что наугад взятая деталь окажется бездефектной.
490. Два брата входят в состав двух спортивных команд, состоящих из 12 человек каждая. В двух урнах имеются по 12 билетов с номерами от 1до 12. Члены каждой команды вынимают наудачу по одному билету из определенной урны (без возвращения). Найти вероятность того, что оба брата вытащат билет номер 6.
491 - 500. Задан закон распределения случайной величины X – размер деталей, выпускаемых заводом ( в первой строке таблицы даны возможные значения измеренной детали, а во второй строке указаны вероятности p этих возможных значений).
Найти: 1) математическое ожидание M(X); 2) дисперсию D(X); 3) среднее квадратическое отклонение 
.
| 491. | X | ||||
| P | 0.3 | 0.2 | 0.4 | 0.1 | |
| 492. | X | ||||
| P | 0.2 | 0.4 | 0.3 | 0.1 | |
| 493. | X | ||||
| P | 0.2 | 0.2 | 0.5 | 0.1 | |
| 494. | X | ||||
| P | 0.1 | 0.5 | 0.3 | 0.1 | |
| 495. | X | ||||
| P | 0.2 | 0.4 | 0.3 | 0.1 | |
| 496. | X | ||||
| P | 0.1 | 0.5 | 0.2 | 0.2 | |
| 497. | X | ||||
| P | 0.1 | 0.2 | 0.5 | 0.2 | |
| 498. | X | ||||
| P | 0.1 | 0.4 | 0.2 | 0.3 | |
| 499. | X | ||||
| P | 0.1 | 0.3 | 0.4 | 0.2 | |
| 500. | X | ||||
| P | 0.2 | 0.4 | 0.3 | 0.1 | |
| 501. | X | ||||
| P | 0,2 | 0,3 | 0,1 | 0,4 | |
| 502. | X | ||||
| P | 0,2 | 0,3 | 0,4 | 0,1 | |
| 503. | X | ||||
| P | 0,2 | 0,3 | 0,1 | 0,4 | |
| 504. | X | ||||
| P | 0,2 | 0,1 | 0,5 | 0,2 | |
| 505. | X | ||||
| P | 0,1 | 0,2 | 0,4 | 0,3 | |
| 506. | X | ||||
| P | 0,2 | 0,3 | 0,4 | 0,1 | |
| 507. | X | ||||
| P | 0,3 | 0,5 | 0,1 | 0,1 | |
| 508. | X | ||||
| P | 0,1 | 0,4 | 0,3 | 0,2 | |
| 509. | X | ||||
| P | 0,1 | 0,2 | 0,2 | 0,5 | |
| 510. | X | ||||
| P | 0,1 | 0,3 | 0,2 | 0,4 | |
511 - 520. Найти доверительный интеграл для оценки математического ожидания а нормального распределения с надежностью 0,95 зная выборочную среднюю 
, объем выборки n и среднее квадратическое отклонение σ.
511. 
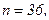
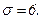
512. 
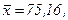
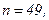
513. 
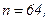
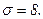
514. 
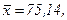
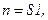
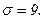
515. 
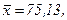
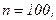
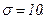
516. 
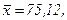
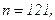
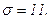
517. 
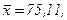
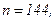
518. 
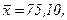
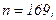
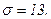
519. 
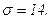
520. 
