Условие Липшица
Для определения глобального экстремума можно использовать равномерную сетку с достаточно мелким шагом (метод перебора). Однако такой подход требует слишком большого времени счета. Чтобы избежать этого, можно использовать некоторые априорные сведения о характере критерия оптимальности, позволяющие изменять шаг в процессе поиска в зависимости от ранее вычисленных значений. С этой целью можно использовать условие Липшица.
Определение. Функция ¦(x) удовлетворяет условию Липшица в области G, если существует такая постоянная величина L > 0 (константа Липшица), что для любых двух векторов x 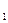 , x
, x  Î G выполняется неравенство
Î G выполняется неравенство
|¦(x 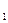 ) - ¦(x
) - ¦(x  )| £ L|x
)| £ L|x 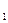 - x
- x  | (5.8)
| (5.8)
Это условие означает, что ¦(x) убывает и возрастает не быстрее линейной функции с заданным коэффициентом L.
З а м е ч а н и я :
1. Если неравенство (5.8) выполняется с константой L, то оно справедливо и при всех L  > L. Поэтому для функции, удовлетворяющей условию Липшица, существует бесконечное множество констант L из (5.8).
> L. Поэтому для функции, удовлетворяющей условию Липшица, существует бесконечное множество констант L из (5.8).
При использовании алгоритмов минимизации, включающих L как параметр, наилучшие результаты достигаются, как правило, если в качестве L берется минимальная из констант Липшица.
2. Из условия (5.8) непосредственно следует непрерывность ¦(x) на отрезке [a; b]. Поэтому, согласно теореме Вейерштрасса, функция ¦(x), удовлетворяющая на отрезке [a; b] условию Липшица, имеет на нем хотя бы одну точку минимума.
3. Условие (5.8) означает, что модуль углового коэффициента любой хорды графика ¦(x) не превосходит L.
Переходя в (5.8) к пределу при |x1 - x2|®0, убеждаемся, что если в некоторой точке существует касательная к графику функции ¦(x), то модуль ее углового коэффициента также не может превышать L. Так, функция ¦(x) =  на отрезке [0; 1] условию Липшица не удовлетворяет, потому что при x®+0 угловой коэффициент касательной к ее графику k неограниченно возрастает (рис. 5.8).
на отрезке [0; 1] условию Липшица не удовлетворяет, потому что при x®+0 угловой коэффициент касательной к ее графику k неограниченно возрастает (рис. 5.8).
4. Если функция ¦(x) имеет на отрезке [a; b] непрерывную производную, то она удовлетворяет на этом отрезке условию Липшица с константой L = max|¦  (x)|.
(x)|.

Рис. 5.8. График функции ¦(x) =  , xÎ[0; 1], не влетворяющей условию Липшица
, xÎ[0; 1], не влетворяющей условию Липшица
По формуле конечных приращений для произвольных точек x 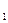 , x
, x  Î[a; b] имеем:
Î[a; b] имеем:
¦(x 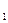 ) - ¦(x
) - ¦(x  ) = ¦
) = ¦  (x)(x
(x)(x 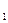 -x
-x  ),
),
где x – некоторая точка, лежащая между x 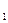 и x
и x  . Отсюда с учетом условия |¦
. Отсюда с учетом условия |¦  (x)| £ max|¦
(x)| £ max|¦  (x)| = L получаем неравенство (5.9) для ¦(x).
(x)| = L получаем неравенство (5.9) для ¦(x).
5. Если a = x  < x
< x 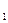 <…< x
<…< x  = b, а функция ¦(x) непрерывна на [a; b] и удовлетворяет условию (5.9) на каждом из отрезков [x
= b, а функция ¦(x) непрерывна на [a; b] и удовлетворяет условию (5.9) на каждом из отрезков [x 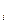 ; x
; x  ], i = 0,1,…, n-1, с константой L
], i = 0,1,…, n-1, с константой L 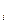 , то она удовлетворяет условию Липшица и на всем отрезке [a; b] с константой
, то она удовлетворяет условию Липшица и на всем отрезке [a; b] с константой 
Использование условия Липшица позволяет ускорить процедуру детерминированного перебора значений проектируемых параметров при определении критерия оптимальности. На рис. 5.9. представлена функция одной переменной, удовлетворяющая условию Липшица на отрезке 0 £ x £ a с константой L  . После того, как найден локальный минимум x
. После того, как найден локальный минимум x  функции ¦(x), удается ускорить поиск остальных локальных минимумов по сравнению с полным перебором на равномерной сетке.
функции ¦(x), удается ускорить поиск остальных локальных минимумов по сравнению с полным перебором на равномерной сетке.

Рис. 5.9. Функция, удовлетворяющая условию Липшица
Пусть h  – некоторый шаг, осуществленный из точки локального минимума x
– некоторый шаг, осуществленный из точки локального минимума x  . Если в точке x
. Если в точке x  + h
+ h  значение функции ¦ не меньше, чем в точке x
значение функции ¦ не меньше, чем в точке x  , т.е. ¦(x
, т.е. ¦(x  +h
+h  ) ³ ¦(x
) ³ ¦(x  ), то, исходя из условия (5.8), можно определить ближайшую точку, в которой функция ¦(x) может достигнуть значения ¦(x
), то, исходя из условия (5.8), можно определить ближайшую точку, в которой функция ¦(x) может достигнуть значения ¦(x  ) (подозрительного на глобальный минимум).
) (подозрительного на глобальный минимум).
Действительно, согласно (5.8) функция ¦(x) убывает не быстрее, чем линейная функция:
j(x) = ¦(x  . +h
. +h  )+L
)+L  [x - (x
[x - (x  + h
+ h  )].
)].
Отсюда следует, что точка x  , в которой необходимо произвести новое пробное вычисление функции ¦(x), может быть получена из условия
, в которой необходимо произвести новое пробное вычисление функции ¦(x), может быть получена из условия
j(x) = ¦(x  ),
),
т.е.
x  = (x
= (x  +h
+h  ) +
) +  (5.9)
(5.9)
Поскольку ¦(x  ) ³ ¦(x
) ³ ¦(x  ) (рис. 5.9), к ней также можно применить сформулированный выше алгоритм для определения следующей пробной точки x
) (рис. 5.9), к ней также можно применить сформулированный выше алгоритм для определения следующей пробной точки x  .
.
В точке x  выполняется равенство ¦(x
выполняется равенство ¦(x  ) = ¦(x
) = ¦(x  ), поэтому из нее производится поиск локального минимума одним из известных методов. В точке x
), поэтому из нее производится поиск локального минимума одним из известных методов. В точке x  достигается значение меньшее, чем ¦(x
достигается значение меньшее, чем ¦(x  ), поэтому все дальнейшие шаги до конца отрезка определяются исходя из ¦(x
), поэтому все дальнейшие шаги до конца отрезка определяются исходя из ¦(x  ). Ввиду того, что не оказывается новых точек, подозрительных на глобальный оптимум, поиск заканчивается.
). Ввиду того, что не оказывается новых точек, подозрительных на глобальный оптимум, поиск заканчивается.