Метод перебора
Численные методы решения задач одномерной оптимизации
Задача оптимизации, в которой целевая функция задана функцией одной переменной, относится к наиболее простому типу оптимизационных задач. Это связано не только с тем, что именно такие задачи обычно решаются в инженерной практике, но и с тем, что одномерные методы оптимизации часто используются для анализа подзадач, которые возникают при реализации итеративных процедур, ориентированных на решение многомерных задач оптимизации.
Для решения задачи минимизации функции ¦(x) на отрезке [a; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью в результате определения конечного числа значений функции ¦(x) и ее производных в некоторых точках отрезка [a; b]. Методы, использующие только значения функции и не требующие вычисления ее производных, называютсяпрямыми методами минимизации.
Прямые методы
Большим достоинством прямых методов является то, что от целевой функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы прямых методов оптимизации, это возможность определения значений ¦(x) в заданных точках.
Рассмотрим наиболее распространенные на практике прямые методы поиска точки минимума. Самым слабым требованием на функцию ¦(x), позволяющим использовать эти методы, является ее унимодальность. Поэтому далее будем считать функцию ¦(x) унимодальной на отрезке [a; b].
Метод перебора
Метод перебора (пассивная стратегия поиска) является простейшим из прямых методов оптимизации.
Пусть
¦(x) Î Q[a; b],
где Q[a; b] – множество унимодальных функций на отрезке [a; b]. Требуется найти какую–либо из точек минимума x  функции ¦(x) на отрезке [a; b] с абсолютной погрешностью e > . Разобьем [a; b] на n равных частей точками деления
функции ¦(x) на отрезке [a; b] с абсолютной погрешностью e > . Разобьем [a; b] на n равных частей точками деления
x 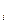 = a+i
= a+i  , i = 0, 1, 2,…, n,
, i = 0, 1, 2,…, n,
где n ³  .
.
Вычислив значения ¦(x) в этих точках, путем сравнения найдем точку x  , для которой
, для которой
¦(x  ) = min¦(x
) = min¦(x 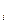 ), 0 £ i £ n.
), 0 £ i £ n.
Далее полагаем x  » x
» x  , ¦
, ¦  » ¦(x
» ¦(x  ). При этом максимальная погрешность e
). При этом максимальная погрешность e  определения точки x
определения точки x  равна e
равна e  = (b-a)/n.
= (b-a)/n.
Пример 5.1.Найти минимальное значение ¦  и точку минимума x
и точку минимума x  функции ¦(x) = x
функции ¦(x) = x 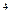 + 8x
+ 8x 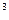 - 6x
- 6x  - 72x на отрезке [1,5; 2,0]. Точку x
- 72x на отрезке [1,5; 2,0]. Точку x  найти с погрешностью e = 0,05.
найти с погрешностью e = 0,05.
¦(x)Î Q[1,5; 2,0], так как ¦¢¢(x) = 12x  + 48x – 12 > 0 при xÎ [1,5; 2].
+ 48x – 12 > 0 при xÎ [1,5; 2].
Выбрав n =  = 10, вычислим значения ¦(x
= 10, вычислим значения ¦(x 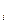 ), x
), x 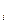 = 1,5 + i 0,05, i = 0,1,…,10, поместив их в таблицу 5.1.
= 1,5 + i 0,05, i = 0,1,…,10, поместив их в таблицу 5.1.
| хi | 1,50 | 1,55 | 1,60 | 1,65 | 1,70 | 1,75 | 1,80 | 1,85 | 1,90 | 1,95 | 2,00 |
¦(x 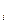 ) )
| -89,4 | -90,2 | -91,2 | -91,8 | -92,08 | -92,12 | -91,9 | -91,4 | -90,5 | -89,4 | -88,0 |
Таблица 5.1
Значения функции f(xi)
Из таблицы 5.1 находим x  » 1,75, ¦
» 1,75, ¦  » -92,12.
» -92,12.