Оценивание параметров линейной модели в модуле Множественная регрессия
Модуль позволяет построить линейную по параметрам модель, используя стандартную процедуру расчета оценок параметров и шаговые алгоритмы.
При использовании стандартного алгоритма оценивания следует выполнить следующие действия:
1. Открыть таблицу с исходными данными (рис.3.7.), которые могут быть импортированы или смоделированы в пакете. В приведенной таблице присутствуют смоделированные измерения входных факторов, отклика и рассчитанные значения предложенных базисных функций для модели второго порядка по управляемым факторам.
Рис. 3.7. Таблица с исходными данными
· в горизонтальном меню выбрать позицию «Анализ», а затем модуль «Множественная регрессия». На стартовой панели модуля выбрать закладку «Дополнительно» и указать зависимую переменную (Y) и независимые переменные (все остальные);
· нажать кнопку ОК и получить окно с результатами вычислений – «Результаты множественной регрессии».
В верхней части окна содержится основная информация об исходных данных и результатах оценивания: имя зависимой переменной количество наблюдений; коэффициент детерминации; оценка множественного коэффициента корреляции, скорректированный коэффициент детерминации; выборочное значение F-статистики, используемой для проверки гипотезы о значимости регрессии в целом, число степеней свободы ( 
), значение вероятности (р), связанной с выборочным значением F, стандартная ошибка оценки – оценка среднеквадратического остаточного отклонения, оценка свободного члена в модели; стандартная ошибка оценки свободного члена регрессии; выборочное значение t-статистики и вычисленное значение уровня значимости р для свободного члена, используемые для проверки гипотезы о значимости свободного члена.
В нижней части окна высвечиваются значимые (красный цвет) и незначимые (синий цвет) оценки стандартизованных коэффициентов регрессии.
· кнопкой Итоговая таблица регрессии открыть окно с более подробным описанием результатов расчетов; в окне приведены оценки параметров для нормированных и ненормированных исходных данных, соответствующие им среднеквадратические отклонения, значения t-статистик и уровней значимости.
В нижней части основного окна STATISTICA щелкнуть по панели «Множественная регрессия» и вернуться в окно с результатами расчетов для продолжения их анализа; возможности анализа представлены на панели «Дополнительно».
· кнопкой Дисперсионный Анализ (ANOVA)открыть таблицу с суммами квадратов и оценками соответствующих дисперсий.
В пакете STATISTICA реализован алгоритм шаговой регрессии с включением и с исключением переменных, которые используют процедуру выметания расширенной матрицы. Результаты оценивания отображаются в выметенной матрице, матрице избыточности, матрице итоговых расчетов по шагам и некоторых других, как будет показано в тестовой задаче.
Шаговый алгоритм оценивания регрессии с использованием процедуры выметания. Тестовая задача ─ реализация шагового алгоритма с включением. В качестве исходных данных используются файл, который получен с помощью проведения активно-пассивного эксперимента на модели для двух управляемых и двух неуправляемых входных факторов.
1. На стартовой панели модуля отметить «Пошаговая или гребневая регрессия», указать зависимые и независимые переменные и нажать «ОК»; на открывшейся панели выбрать «Пошаговая», а затем «Пошаговая с включением»,
2. На следующей панели указать значения F-статистик для включения (F=4) и исключения (F=3,8), число шагов в процедуре оценивания (10) и способ отображения результатов (на каждом шаге) ,
3. Определение наиболее сильно коррелированного с откликом входного фактора 
или базисной функции проводится автоматически, после запуска модуля, после чего проводится выметание расширенной матрицы по i-ому ведущему элементу ( 
) для включения в модель; поскольку частное F-отношение 
, то для выбора можно анализировать значения 
-статистик; по всем показателям наиболее значима и сильно связана с откликом базисная функция U2U2, которая включается на первом шаге.
Результат выметания представляется в виде результатов оценивания,
ШАГ 1
Результаты множ. регрессии(Шаг 1)
Зав.перем.:Y Множест. R = ,82415121 F = 91,05044
R2= ,67922522 сс = 1,43
Число набл.: 45 скоррект.R2= ,67176534 p = ,000000
Стандартная ошибка оценки:1050,4157662
Своб.член: 1868,0069535 Ст.ошибка: 271,2162 t( 43) = 6,8875 p = ,0000
U2U2 бета=,824
(F–статистика со степенями свободы ٧1,٧2 для проверки значимости уравнения в целом, t–статистика для проверки значимости свободного члена, p– сооветствующий ей уровень значимости )
Рис.3.8. Результаты пошаговой регрессии на первом шаге
4. Матрицы анализируются для выбора базисных функций на последующее включение или исключение. Обычно циклически повторяются следующие процедуры:
a. Анализируется величина толерантности ( 
) для всех переменных, у которых она больше некоторой пороговой границы, т.е. они не слишком сильно коррелированны с iпеременными включенными ранее;
b. Рассчитываются величины 
где где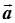 
– нормированный вектор оценок регрессии, 
- диагональный элемент матрицы 
; при этом для переменных не включенных в регрессию величина 
и положительна, а для переменных, включенных в регрессию 
;
c. Для определения, имеются ли переменные для включения в регрессию, среди всех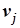 
находится 
, которое сравнивается с критическим значением 
, где 
– критическое значение статистики 
на включение; j-ый регрессор включается в уравнение, если 
;
d. Для определения, имеются ли среди включенных ранее регрессоры, которые могут быть удалены, находят 
, которое сравнивается с критическим значением 
, где 
– критическое значение 
статистики на исключение; j-ый регрессор исключается из уравнение, если 
.
На каждом шаге желательно не исключать регрессор, введенный на предыдущем шаге, что достигается автоматически при установке пользователем 
.
5. В пакете STATISTICA действия на каждом шаге алгоритма оценивания реализуется автоматически. Далее представлен пример применения алгоритма пошаговой обработки в режиме «Пошаговый с включением».
На каждом шаге следует кнопкой Избыточность (Redundancy) открывать таблицу, в которой представлены текущие значения R2 , толерантности, частных корреляций и анализировать действия на текущем и следующем шаге.
ШАГ 2.Анализ таблицы3.8 показывает, что в результате включения базисной функции U2U2 в модель наибольшей толерантностью и наибольшим частным коэффициентом корреляции обладает базисная функция X1U1, которая и включается в модель на втором шаге.
Результаты множ. регрессии(Шаг 2)
Зав.перем.:Y Множест. R = ,97769050 F = 454,9608
R2= ,95587872 сс = 2,42
Число набл.: 45 скоррект.R2= ,95377771 p = 0,000000
Стандартная ошибка оценки:394,18015863
Своб.член: 1908,7082184 Ст.ошибка: 101,8078 t( 42) = 18,748 p = 0,0000
U2U2 бета=,803 X1U1 бета=,526
Рис. 3.9. Результаты пошаговой регрессии на втором шаге