Последовательность униполярных треугольных импульсов
Рис. 3.9. Треугольное колебание, сумма первых пяти гармоник и ошибка аппроксимации -
на нижнем графике, для наглядности увеличена в 10 раз
Ряд Фурье для этой функции имеет следующий вид:
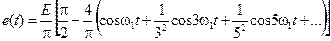(3.40)
В нем так же отсутствуют четные гармоники.
Отметим, что амплитуды гармоник убывают более быстро, чем в предыдущих случаях. Это объясняется отсутствием точек разрыва (скачков) функции.
Примечание: Симметричный (середина
импульса при t=0) импульс длительности Tu, амплитуда которого равна 1, обозначают D(t,Tu). Такой импульс можно представить в виде свертки двух одинаковых прямоугольных импульсов длительностью Ти/2:
