Средние величины вариационного ряда

Основной характеристикой вариационного ряда является его средняя арифметическая, называемая такжевыборочной средней.

Для дискретного выборочного ряда средняя арифметическая равна ,

а для интервального ряда

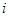В последней формуле за принимают середину –го интервала.

Вариационным размахом называется число

Выборочной дисперсией называется средняя арифметическая квадратов отклонений вариант от их выборочной средней:

где – это значение варианта для дискретного ряда или середина i-го интервала для интервального ряда.

Для практических вычислений более удобной является следующая формула:

Свойства:

1. Дисперсия постоянной равна нулю.

2. Если ко всем вариантам добавить постоянное число, то дисперсия не изменится.

3. Если все варианты умножить на одно и то же число , то дисперсия умножится на .

4. (Правило сложения дисперсий).

Пусть значения выборки разбиты на групп. Обозначим через количество различных вариант в й группе, через - частоту -й варианты в этой группе. Тогда я группа ряда записывается в виде , при этом значение повторяется раз. Обозначим через групповые средние арифметические: .

Групповые дисперсии равны .

Средняя арифметическая групповых дисперсий равна

.

Межгрупповая дисперсия равна .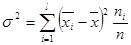

Правилом сложения дисперсий называется равенство

Оно служит основой для дисперсионного анализа.

Мерой вариации признака является выборочное среднее квадратическое отклонение, которое определяется как корень из дисперсии:

В статистическом анализе рассматривается также коэффициент вариации, равный процентному отношению выборочного среднего квадратического отклонения к выборочной средней: