Линейная зависимость и независимость векторов.

Определение. Совокупность всевозможных n-мерных векторов с действительными координатами называется n-мерным векторным пространством и обозначается .

Определение.Линейной комбинацией векторов называется сумма вида

,

где - действительные числа , называемые коэффициентами.

Линейная комбинация векторов также является вектором, так как она образуется из них с помощью операций сложения и умножения на число.

Определение. Система векторов называется линейно зависимой, если существует равная нулю линейная комбинация этих векторов, т.е. , в которой хотя бы один из коэффициентов отличен от нуля.

Если же все коэффициенты 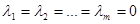, то система векторов называется линейно независимой.

На вопрос о линейной зависимости или независимости системы векторов иногда можно ответить, используя следующие теоремы:

Теорема 1. Для того, чтобы система векторов была линейно зависимой, необходимо и достаточно, чтобы хотя бы один из них был представлен в виде линейной комбинации остальных.

Теорема 2. В n-мерном пространстве любая система, содержащая более чем n векторов, является линейно зависимой.

Теорема 3.Если определитель, составленный из координат векторов, отличен от нуля, то система векторов линейно независима. Если указанные теоремы не дают ответа на вопрос о линейной зависимости или независимости векторов, то необходимо решать систему уравнений относительно , либо определять ранг системы векторов.