Лекция №2 «Главные оси и главные моменты инерции
Рассмотрим, как изменяются моменты инерции при повороте координатных осей. Положим, даны моменты инерции некоторого сечения относительно осей 0х, 0у (не обязательно центральных)- ,
, 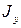 - осевые моменты инерции сечения. Требуется определить
- осевые моменты инерции сечения. Требуется определить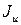 ,
, 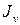 - осевые моменты относительно осей u, v, повёрнутых относительно первой системы на угол
- осевые моменты относительно осей u, v, повёрнутых относительно первой системы на угол 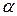 (рис. 8)
(рис. 8)
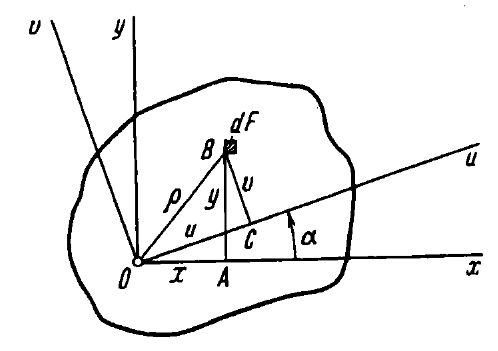
Рис. 8
Так как проекция ломаной линии ОАВС равна проекции замыкающей, находим:
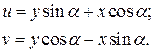 (15)
(15)
Исключим u и v в выражениях моментов инерции:
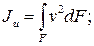
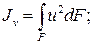

Тогда

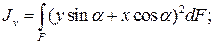
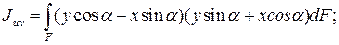
Откуда
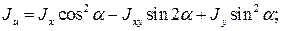 (16)
(16)
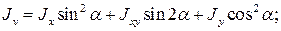 (17)
(17)
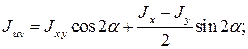 (18)
(18)
Рассмотрим два первых уравнения. Складывая их почленно, получим
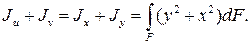
Таким образом, сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей не зависит от угла 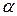 и при повороте осей остается постоянной. Заметим при этом, что
и при повороте осей остается постоянной. Заметим при этом, что
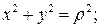
Где  - расстояние от начала координат до элементарной площадки (см. рис.5). Таким образом
- расстояние от начала координат до элементарной площадки (см. рис.5). Таким образом
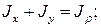
Где  - уже знакомый нам полярный момент инерции:
- уже знакомый нам полярный момент инерции:

Определим осевой момент инерции круга относительно диаметра.
Так как в силу симметрии  но, как известно,
но, как известно, 
Следовательно, для круга

С изменением угла поворота осей 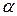 значения моментов
значения моментов 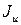 и
и 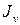 меняются, но сумма остается неизменной. Следовательно существует такое значение
меняются, но сумма остается неизменной. Следовательно существует такое значение 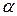 , при котором один из моментов инерции достигает своего максимального значения, в то время как другой момент принимает минимальное значение. Дифференцируя выражение
, при котором один из моментов инерции достигает своего максимального значения, в то время как другой момент принимает минимальное значение. Дифференцируя выражение 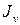 по углу
по углу 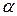 и приравнивая производную к нулю, находим
и приравнивая производную к нулю, находим
 (19)
(19)
При этом значении угла 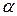 один из осевых моментов будет наибольшим, а другой - наименьшим. Одновременно центробежный момент инерции
один из осевых моментов будет наибольшим, а другой - наименьшим. Одновременно центробежный момент инерции  обращается в нуль, что можно легко проверить, приравнивая к нулю формулу для центробежного момента инерции
обращается в нуль, что можно легко проверить, приравнивая к нулю формулу для центробежного момента инерции  .
.
Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными осями. Если они к тому же являются центральными (точка начала координат совпадает с центром тяжести сечения), то тогда они называются главными центральными осями (u; v). Осевые моменты инерции относительно главных осей называются главными моментами инерции - 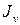 и
и 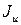
И их значение определяется по следующей формуле:
 (20)
(20)
Знак плюс соответствует максимальному моменту инерции, знак минус - минимальному.
Существует ещё одна геометрическая характеристика – радиус инерциисечения. Эта величина часто используется в теоретических выводах и практических расчётах.
Радиусом инерции сечения относительно некоторой оси, например 0x, называется величина  ,определяемая из равенства
,определяемая из равенства
 (21)
(21)
F – площадь поперечного сечения,
 - осевой момент инерции сечения,
- осевой момент инерции сечения,
Из определения следует, что радиус инерции равен расстоянию от оси 0х до той точки, в которой следует сосредоточить (условно) площадь сечения F, чтобы момент инерции одной этой точки был равен моменту инерции всего сечения. Зная момент инерции сечения и его площадь, можно найти радиус инерции относительно оси 0х :
 (22)
(22)
Радиусы инерции, соответствующие главным осям, называются главными радиусами инерции и определяются по формулам

 (23)
(23)