Внедренные диаграммы и листы диаграмм
Диаграмму можно создать на отдельном листе или поместить в качестве внедренного объекта на лист с данными. Независимо от способа размещения диаграмма является связанной с исходными данными на листе, то есть при обновлении данных обновляется и созданная на их основе диаграмма.
Внедренные диаграммы Внедренная диаграмма рассматривается как графический объект и сохраняется в качестве части листа, на котором она создана. Внедренные диаграммы следует использовать в случаях, когда требуется отобразить или напечатать одну или несколько диаграмм вместе с данными листа.
Листы диаграмм. Лист диаграммы — это отдельный лист в книге, имеющий собственное имя. Листы диаграмм следует использовать в случаях, когда требуется просмотреть или изменить большие или сложные диаграммы отдельно от данных, или когда требуется сохранить пространство экрана для работы с листом.
Построение диаграмм.
Большинство диаграмм строятся в прямоугольной системе координат. По горизонтальной оси Х откладываются значения независимой переменной (аргумента), а по вертикальной оси Y – значения зависимой переменной (функции). На один рисунок может быть выведено одновременно несколько диаграмм.
При графической обработке числовой информации с помощью ТП следует:
1. указать область данных (блок клеток), по которым будет строиться диаграмма;
2. определить последовательность выбора данных (по строкам или по столбцам) из выбранного блока клеток.
При выборе по столбцам Х-координаты берутся из крайнего левого столбца выделенного блока клеток. Остальные столбцы содержат Y-координаты диаграмм. По количеству столбцов определяется количество строящихся диаграмм. При выборе по строкам самая верхняя строка выделенного блока клеток является строкой Х-координат, остальные строки содержат Y-координаты диаграмм.
Рассмотрим диаграммы 5 различных типов: круговые, столбчатые, ярусные, линейные и областные. На самом деле типов диаграмм гораздо больше. Но эти наиболее распространенные.
I. Круговая диаграмма служит для сравнения нескольких величин в одной точке. Особенно полезна она, если величины в сумме составляют нечто целое (100%). Круговая диаграмма не всегда обеспечивает необходимую наглядность представления информации. Во-первых, на одном круге может оказаться слишком много секторов. Во-вторых, все сектора могут быть примерно одинакового размера. Вместе эти две причины делают круговую диаграмму малополезной.
II. Столбчатая диаграмма служит для сравнения нескольких величин в нескольких точках. Данные диаграммы состоят из столбиков. Высота столбиков определяется значениями сравниваемых величин, каждый столбик привязан к некоторой опорной точке. Отличие столбчатой диаграммы, построенной для сравнения сразу несколько данных от столбчатой диаграммы, где будет отображена одна величина, лишь в том, что у каждой опорной точке будет стоять не один столбик, а несколько. Все столбцы одной величины закрашены в один цвет.
III. Линейная диаграмма служит для того, чтобы проследить за изменениями нескольких величин при переходе от одной точки к другой. Построение линейной диаграммы аналогично построению столбчатой. Но вместо столбиков просто отмечается их высота (точками, черточками, крестиками – неважно) и полученные отметки соединяются прямыми линиями (диаграмма – линейная). Вместо разной штриховки (закраски) столбиков используются разные отметки (ромбики, треугольники, крестики и т.д.), разная толщина и типы линий (сплошная, пунктирная и т.п.), разный цвет.
IV.Ярусная диаграмма позволяет наглядно сравнивать суммы нескольких величин в нескольких точках, и при этом показывать вклад каждой величины в общую сумму. Порядок построения ярусной диаграммы очень напоминает порядок построения диаграммы столбчатой. Разница лишь в том, что столбики в ярусной диаграмме ставятся не рядом друг с другом, а один на другой. Соответственно меняются правила расчета вертикального и горизонтального размера диаграммы. Вертикальный размер будет определяться не наибольшей величиной, а наибольшей суммой величин. Зато количества столбиков всегда будет равняться количеству опорных точек: в каждой опорной точке всегда будет стоять ровно один многоярусный столбик.
V. Областная диаграмма (диаграмма площадей) – гибрид ярусной диаграммы с линейной. Позволяет одновременно проследить изменение каждой из нескольких величин и изменение их сумм в нескольких точках. Отдельные столбики здесь сливаются, образуя непрерывные области. Отсюда и название – диаграмма областей или диаграмма площадей. Каждая область соответствует какой-то одной величине, для указания на которую используется различная штриховка (раскраска). Раньше ярусами располагались столбики, теперь – линии (и очерченные ими площади).
Построение простого графика:
1. Создадим таблицу значений и построим график функции,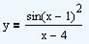 
с шагом 0.2, если хÎ[-3;3].
Для этого столбец А обозначим как х, а столбец В – как у.
В ячейку А2 занесем первое значение для х, в нашем случае оно будет равно –3. В ячейку А3 занесите второе значение, которое вычисляется как первое значение + шаг = –3+0.2 = –2.8.Затем выделим одновременно ячейки А2:А3для того, чтобы заполнить последовательность значений х. Установим указатель мыши в правом нижнем углу ячейки А3 и после появления черного крестика удерживая нажатой левую клавишу мыши, растянем значение аргумента до требуемой величины – 3. Если верно растягивать значения аргумента, то справа от креста должно появляться текущее значение х в виде примечания (см. рис.1).
В ячейку В2 необходимо записать функцию, того графика, который мы хотим построить. Запись любой формулы начинается со знака равенства. Вместо х используется адрес той ячейки, который расположен левее записываемой функции. Если мы записываем формулу для функции в ячейке В2, то вместо х берем адрес ячейки А2, если формулу пишем в В3, то вместо х берем адрес ячейки А3 и т. д. (см. рис.1). После того как формула записана, она копируется во все ячейки, расположенные правее заданных х.Затем, когда таблица значений х и у готова, оба столбца со значениями аргумента и функции выделяются. Для построения графика обратимся к меню Вставка® Диаграмма и выберем вид диаграммы Точечная, после чегонажмем Далее и будем следовать указаниям возникающего диалога. Когда график появится в рабочей книге, переместим его в нужное место.
Построение нескольких графиков на одной координатной плоскости:
2. Создадим таблицу значений и построим на одном шаблоне графики функций y1 = cos(x),
y2 = cos(kx), х изменяется от -p до p с шагом 0.1, k – любое число.
Для помещения двух графиков функций на один шаблон следует для обеих функций задать одинаковые значения для х. В связи с тем, что необходимые значения аргумента расположены в промежутке от от -p до p, воспользуемся соответствующей математической функцией ПИ(), не имеющей аргумента, то есть в скобках после имени функции ничего не пишется. Таким образом, для задания аргумента в ячейку А2 запишем = – ПИ(). Воспользуемся способом заполнения последовательности значений с помощью формулы (см. рис 2). Для этого в ячейку А3 запишем формулу:
= А2+0,1, то есть предыдущее значение последовательности плюс шаг. Будем копировать формулу до тех пор, пока не появится значение наиболее приближенное к p = 3,14.
В столбцы В и С запишем формулы для функций у1 и у2. Обратите внимание на то, что для ввода константы k была использована абсолютная адресация (F4) для того, чтобы при копировании формулы этот адрес не менялся.