Решение.

а)

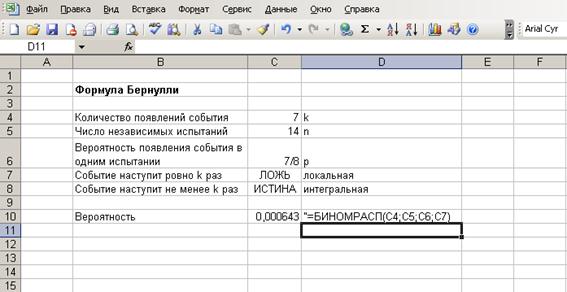
б)

Если число испытаний n достаточно высоко, то для вычисления вероятности того, что событие A наступит ровоно k раз, используется локальная теорема Лапласа.

,

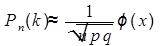где ,

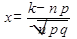
Для определения вероятности применяется функция НОРМРАСП(). Аргументами функции являются количество появлений события k, среднее (математическое ожидание количества появлений события в n испытаниях) 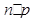, стандартное отклонение (среднее квадратическое отклонение количества появлений события в n испытаниях) 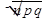( 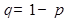), логическая переменная Интегральная, принимающая значение «ЛОЖЬ» если определяется вероятность появления ровно k событий или «ИСТИНА», если определяется вероятность того, что в n испытаниях событие наступит не менее k раз.

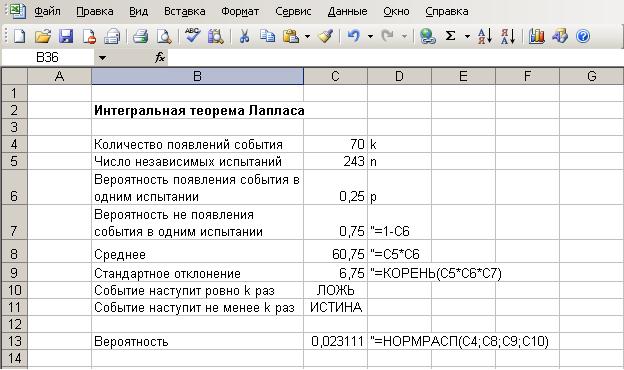
Пример. Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.

Решение.

Если, при достаточно большом числе испытаний, необходимо вычислить вероятность наступления события от k₁ до k₂ раз ( 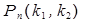), используют интегральную теорему Лапласа:

,

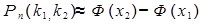где 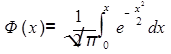- функция Лапласа.

,

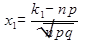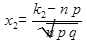
При вычислении данной вероятности в Excel используют формулу:

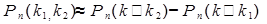
Для определения вероятносте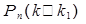й и 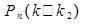также применяется функция НОРМРАСП(), значения переменной Интегральная принимается «ИСТИНА».

Пример. Вероятность появления на занятиях студента равна 0,2. В семестре всего 385 занятий. Какова вероятность того, что студент будет присутствовать не менее чем на 76 занятиях?